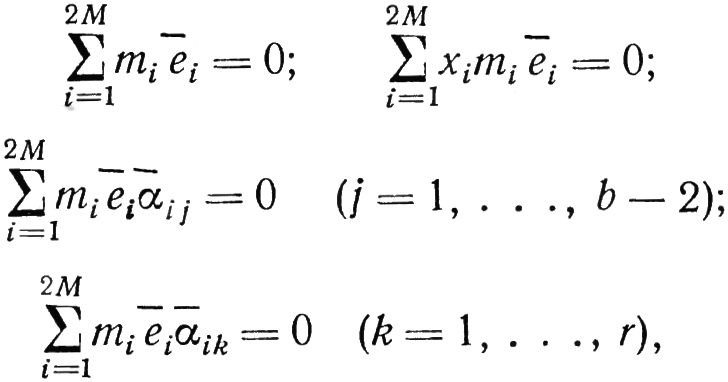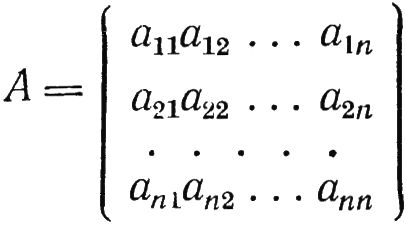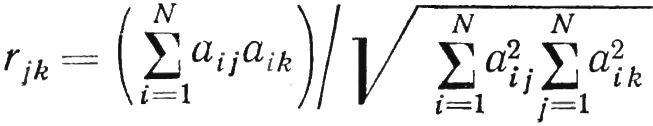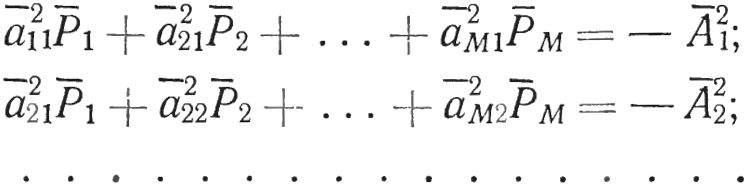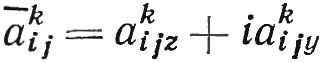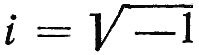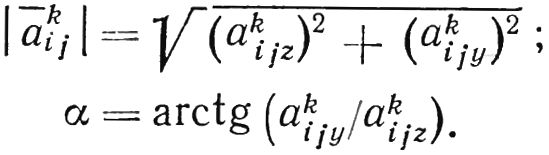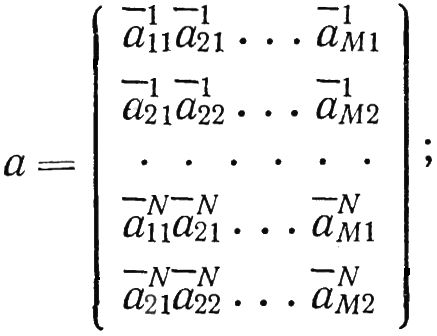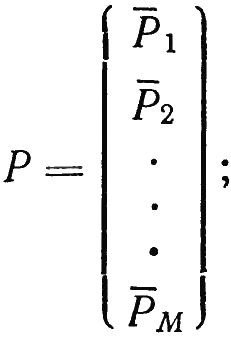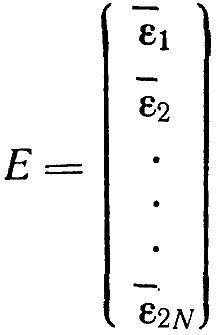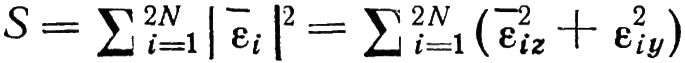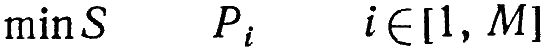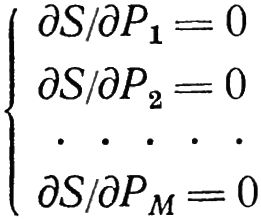Известно, что невесомый ротор турбины с r сосредоточенными массами, который оперт на b подшипники при любом дисбалансе, распределенном как угодно вдоль него, может быть динамически целиком сбалансирован корректирующими массами, которые размещены в M = r + b различных плоскостях по длине ротора турбины, являющимися поверхностями коррекции.
Под полной понимается такая балансировка, когда не возникают динамические реакции ни в одном подшипнике при любой частоте вращения.
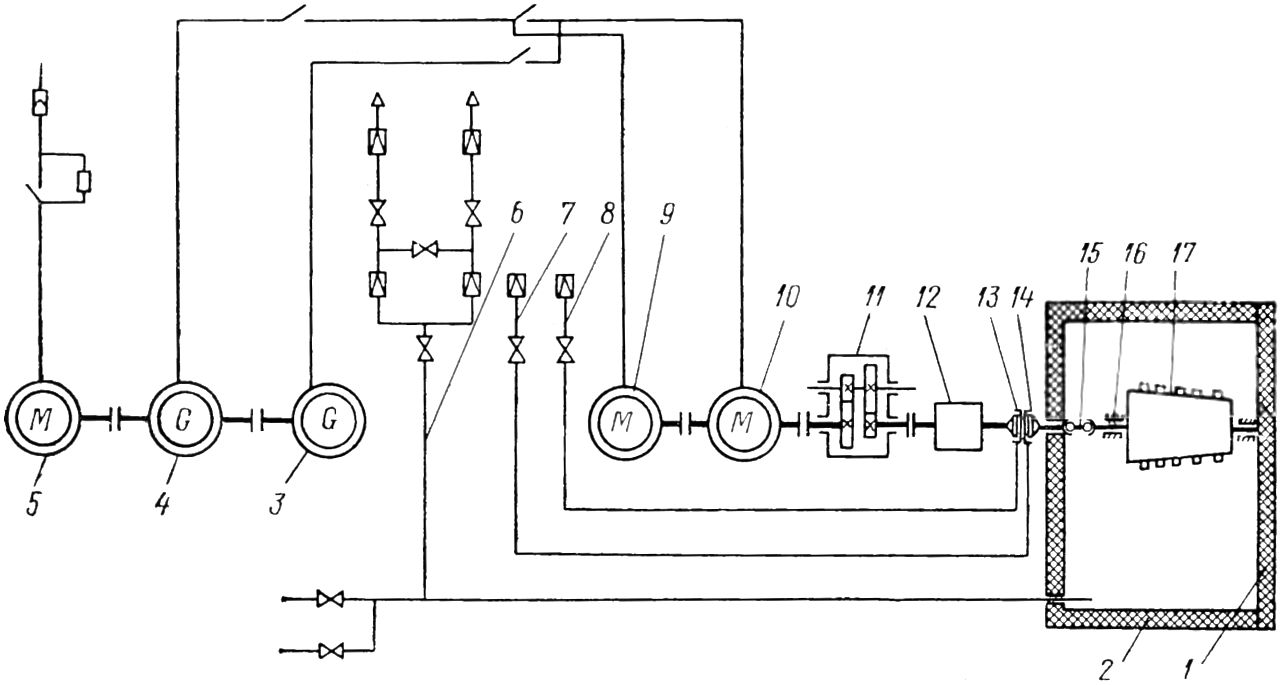
Рис. 15.25. Схема специализированного балансировочного станка для балансировки роторов паровых турбин модели DH-10: 1 — ворота вакуумной камеры; 2 — вакуумная камера; 3,4 — генераторы; 5 — электродвигатель привода генераторов; 6, 7, 8 — вакуумно-воздушные системы; 9, 10 — электродвигатели привода ротора; 11 — повышающий редуктор; 12 — валоповоротное устройство; 13, 14 — воздухоотводящие муфты; 15 — карданное звено; 16 — подшипники; 17 — балансируемый ротор.
При доказательстве приняты два допущения. Все неуравновешенные массы mi, включая корректирующие, малы по сравнению с массами турбинного ротора. Все прогибы yi неуравновешенных масс mi малы по сравнению с модулями эксцентриситетов ei массы и, следовательно, все центробежные силы miω2 (ei + yi) могут быть заменены выражениями:
Со сделанными допущениями в процессе доказательства получается следующая система векторных уравнений применительно к балансировке на станке, схема которого изображена на рис. 15.25:
Где xi — координата x массы mi. Ось X проходит через центры подшипников и имеет начало в центре подшипника, обращенного к карданному валу; ᾱij — комплексный вектор прогиба сечения, где расположена масса mi от единичной центробежной силы, приложенной в сечении, где расположен j-й подшипник; ᾱik — комплексный вектор прогиба сечения, где расположена масса mi от единичной центробежной силы, приложенной в сечении, где помещается k-я основная масса.
Таким образом, получаем определенное выше число 2 + b — 2 + r = M-векторных (двумерных) уравнений с независимыми массами mi.
Если число плоскостей коррекции (и, следовательно, корректирующих масс) меньше значения M, то полное уравновешивание неосуществимо. Если число плоскостей коррекции больше значения M, то у системы бесконечное множество решений.
Выбор числа плоскостей коррекции не может быть произвольным, и он подчинен определенным условиям.
Для двухопорных роторов турбин с эксплуатационным числом оборотов вращения, находящимся между второй и первой критическими частотами, существует лишь пять диапазонов частот вращения, измерения в которых дать могут независимые условия для определения величины и положений корректирующих масс. Внутри каждого диапазона можно получить только уточняющую информацию, так как результаты полученных при этом измерений зависимы друг от друга.
Динамическая балансировка двухопорных роторов паровых турбин по рассматриваемому способу производится на пяти частотах вращения коррекции, каждая из которых находится в диапазонах:
жесткого ротора при nб1 = (0,5÷0,6)n1 кр;
докритическом при nб2 = (0,9÷0,95)n1 кр;
закритическом при nб3 = (1,05÷1,1)n1 кр;
переходном при nб4 = (0,8÷0,85)nэ;
эксплуатационном при nб5 = (1÷1,05)nэ.
Через n1 кр обозначена частота вращения ротора первая критическая, а через nэ — эксплуатационная частота вращения ротора.
Двухопорные турбинные роторы с n1 кр = 1750 об/мин и nэ = 3000 об/мин в связи с вышеизложенным можно балансировать с назначением частот вращения коррекции, об/мин: nб1 = 1000; nб2 = 1650; nб3 = 1900; nб4 = 2500; nб5 = 3000.
Из условия существования пяти, назовем их «независимыми», диапазонов частот вращения следует, что балансировка ротора осуществлена может быть, не свыше, чем в 10 плоскостях коррекции, так как для балансировки ротора внутри каждого диапазона достаточно двух плоскостей коррекции.
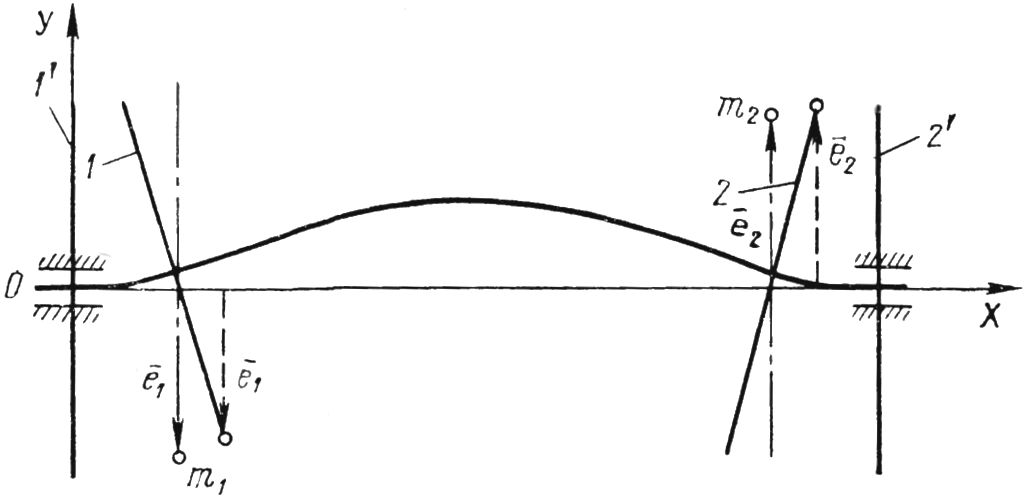
По определению в первом диапазоне ротор паровой турбины является жестким. Необходимо, чтобы плоскостями коррекции такого ротора являлись плоскости симметрии подшипников. Это обусловлено тем, что при переходе в следующие диапазоны частот вращения ротор становится гибким. В самом деле, пусть плоскости коррекции жесткого ротора не совпадают с плоскостями симметрии подшипников. Тогда при любой форме изгиба ротора плоскости коррекции поворачиваются вокруг осей, перпендикулярных плоскости XOY (рис. 15.26). При этом эксцентриситеты изменят свои модули, что приведет к появлению дополнительных дисбалансов, для устранения которых потребуются дополнительные корректирующие массы. В то же время, измерение деформаций подшипников или динамических реакций в рассматриваемом диапазоне с частотой вращения nб1 не может дать информации о распределении дисбалансов ротора турбины в гибком состоянии. И поэтому дополнительные уравнения, соответствующие дополнительным корректирующим массам, не могут быть составлены. Таким образом, только четыре диапазона частот вращения nб2, nб3, nб4 и nб5 определяют распределение дисбаланса по длине ротора.
Рис. 15.26. Положение плоскостей коррекции ротора при его балансировке в режиме жесткого ротора паровой турбины: 1, 2 — плоскости коррекции; 1′, 2′ — плоскости симметрии подшипников, m1, m2 — корректирующие массы; ē1, ē2 — эксцентриситеты корректирующих масс.
Если плоскости симметрии подшипников недоступны в качестве плоскостей коррекции, то балансировка турбинного ротора должна осуществляться не более чем в восьми плоскостях коррекции. Местоположение этих плоскостей следует выбирать исходя из теории собственных форм изгиба, в местах пучностей упругой линии и вблизи опор.
Опыт осуществления балансировки по рассматриваемому методу показывает, что существенное несовпадение даже одной плоскости коррекции с плоскостью, в которой расположен хотя бы незначительный дисбаланс, приводит к резкому росту корректирующих масс в остальных плоскостях и к ухудшению общего результата балансировки. Поэтому при выборе места положения плоскостей коррекции необходимо учитывать конструктивные особенности ротора и располагать плоскости коррекции максимально близко к местам возможного дисбаланса. Плоскости коррекции должны быть на крупных насадных деталях турбин: дисках, полумуфтах, втулках уплотнений.
Опыт балансировки показал также, что наличие плоскостей коррекции на консольных участках является необходимым условием качественной балансировки роторов. При наличии консольных участков необходимо использовать дополнительные плоскости коррекции на этих участках. Отсутствие плоскостей коррекции на консольных участках так же, как и недостаточное количество их в межопорном пролете, приводит к невозможности устранения упругих деформаций в широком диапазоне скоростей, к появлению дополнительных внутренних моментов и к резкому увеличению корректирующих масс. Даже в случае удовлетворительных результатов балансировки при приемлемом уровне остаточных вибраций опор нельзя гарантировать нормальную работу ротора в турбине, когда условия работы консольных участков изменятся.
При расчетах численных значений и положений корректирующих масс на основе работы вводятся характеристические коэффициенты — динамический коэффициент влияния αij и коэффициент чувствительности αij.
В общем случае динамическим коэффициентом влияния называется вектор прогиба в сечении i ротора, вызванного силой центробежной от единичного дисбаланса, приложенного в сечении j при данных частотах вращения ротора паровой турбины.
Коэффициентом чувствительности называется амплитуда вектора скорости колебания (виброскорость) сечения i ротора, вызванного центробежной силой от единичного пробного груза, приложенного в сечении j при данных частотах вращения ротора.
Балансировка по способу коэффициентов чувствительности может быть осуществлена при выполнении условия:
KN ≥ M
Где K — число точек измерения динамических реакций; N — число скоростей коррекции. Это соотношение означает, что число плоскостей коррекции не должно превышать числа независимых измерений KN.
Необходимое число независимых измерений может быть получено при динамической балансировке на балансировочном станке при измерениях только на опорах, но на нескольких скоростях, взятых из разных диапазонов.
Число M плоскостей коррекции очевидно равно числу искомых корректирующих масс, т. е. числу неизвестных. Число KN независимых измерений, очевидно, характеризует независимые условия, т. е. равно числу уравнений.
Если различные измерения производятся в одном диапазоне частот вращения, то, как показывают практические расчеты, получаются так называемые вырожденные системы уравнений, что свидетельствует о наличии линейной зависимости, по меньшей мере, между двумя из них.
Таким образом, учитывая изложенное ранее, для двухопорных роторов паровой турбины можно получить не более чем 2 × 8 = 16 независимых векторных уравнений. Если бы удалось найти 16 корректирующих плоскостей на роторе, вышеприведенное условие обратилось бы в равенство и выведенная система векторных уравнений имела бы единственное решение.
Если число уравнений взять равным числу неизвестных (KN = M), то часто получаются системы с плохо обусловленными матрицами, несмотря на то, что скорости коррекции выбираются из разных диапазонов.
Рассмотрим, например, матрицу:
Предположим, что компоненты каждого вектора-столбца суть значения некоторой случайной величины и что все реализации равновероятны. Тогда статистический коэффициент коррекции между двумя любыми столбцами матрицы A, например j и k, имеет вид:
Была выведена зависимость обусловленности матрицы системы от значения коэффициента корреляции между составлявющими ее векторами. Чем выше коэффициент корреляции, тем больше число обусловленности матрицы A (rjk ϵ [0, 1]).
Известно, что плохо обусловленные системы уравнений приводят к решению, обладающему низкой точностью, т. е. имеющему большую невязку. Расчеты корректирующих масс с помощью таких систем уравнений могут привести к ошибочным результатам.
Для исключения этого предложен расчет корректирующих масс с применением способа наименьших квадратов.
Выбирается N скоростей коррекции из разных диапазонов скоростей. Для двухопорных роторов турбин K = 2. Определяется число М плоскостей коррекции так, чтобы KN > M. Таким образом, число уравнений становится больше числа неизвестных.
Составим систему уравнений для определения корректирующих грузов. Имеем для каждой скорости коррекции по два векторных уравнения динамического равновесия (для каждого подшипника):
1-я скорость:
2-я скорость:
N-я скорость:
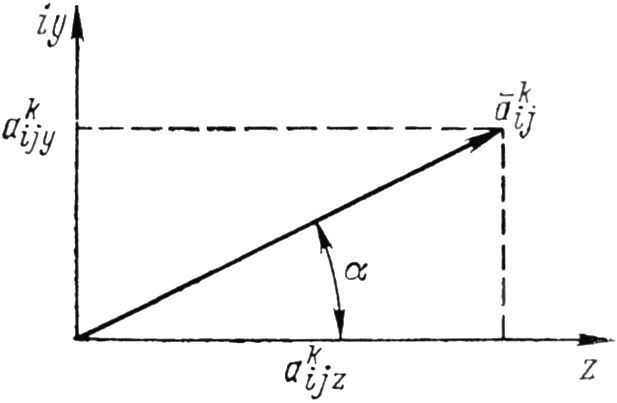
В исходной системе принято: ākij — векторный коэффициент чувствительности, мм/(с·Н) (мм/(с·гс)); Pj — корректирующий груз, Н (гс); Āki — виброскорость, мм/с; j = 1, 2 — номер подшипника; i = 1, …, M — номер плоскости коррекции; k = 1, …, N — номер скорости коррекции. Под вектором здесь понимается комплексная величина, вещественная и мнимая части которой являются составляющими вектора по осям, например (рис. 15.27):
Где неиндексное:
Очевидно, что каждое векторное уравнение рассматриваемой исходной системы эквивалентно двум скалярным. В силу специального определения вектора произведение āijPj имеет смысл и равно обычному произведению комплексных величин.
Рис. 15.27. Графическое построение к определению векторного коэффициента чувствительности.
Из рисунка видно, что:
Рассматриваемая исходная система уравнений переопределена и поэтому несовместна. Следовательно, точное ее решение принципиально не может быть найдено. Задача состоит в том, чтобы минимизировать вектор невязки системы.
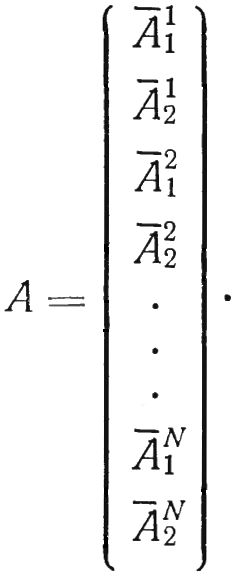
Представим систему уравнений в векторно-матричной форме aP = -A,
Где:
Здесь a — матрица [2N × М ] прямоугольная; P — вектор [M × 1]; A — вектор [2М × 1].
Компоненты матрицы а и векторов P и A — комплексные.
Вектор E = aP + A назовем вектором невязки. Его компоненты, образующиеся по очевидному закону из матрицы исходной системы уравнений, обозначим:
Составим из компонента вектора E следующее выражение:
Где S — квадрат нормы вектора E невязки. Найдем:
Это приводит к системе уравнений с M неизвестными:
Решение этой системы существует и единственно, так как система неоднородная и должна быть невырожденной.
Полученные значения Pi минимизируют вектор невязки E и в этом смысле являются оптимальными, наиточнейшими решениями системы уравнений, приведенной выше.
Для получения численных значений коэффициентов этой системы уравнений производится измерение виброскоростей Āik турбинных подшипников на числе скоростей коррекции N‘ >> N, после чего составляется матрица а размерности [2N×M]. Затем с помощью коэффициента корреляции выбирается 2N наименее коррелированных вектор-строки. В этом и заключается применение способа наименьших квадратов к данной задаче.
В целях реализации описанного алгоритма специалистами ПО «Турбомоторный завод» составлена программа для ЭВМ, используемая при расчетах.
Таким образом, один раз для данной конструкции ротора паровой турбины определяется число и расположение плоскостей коррекции, число и значения скоростей коррекции, а также радиус, на котором должен находиться центр корректирующей массы и угол (фаза), определяющий направление этого радиуса. Число опор, на которых производится динамическая балансировка, всегда равно двум. Значение динамических реакций для каждой из опор (модуль и фаза) в каждом диапазоне частот вращения замеряется непосредственно при балансировке.
По имеющейся информации по программе на ЭВМ определяются значения модуля и фазы радиусов — векторов корректирующих масс.
- Динамическая балансировка роторов паровых турбин: основные определения и используемое оборудование
- Динамическая балансировка роторов паровых турбин с расчетом масс корректирующих грузов итерационным методом
- Пример расчета масс корректирующих грузов итерационным методом при динамической балансировке ротора низкого давления паровой турбины Т-100-130