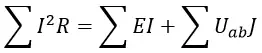Заземление точки схемы
При осуществлении заземления точки схемы её потенциал принимают равным нулю. Распределение токов при этом в схеме не меняется, потому что новые ветви, где могли бы протекать электрические токи, не образуются.
Если же заземлить больше одной точки схемы, потенциалы которых отличаются, то появятся дополнительные ветви через землю. Схема при этом делается отличной от исходной, а распределение электрических токов в ней изменяется.
Расчёт и построение потенциальной диаграммы электрической цепи
Под потенциальной диаграммой электрической цепи понимают график, показывающий распределение электрического потенциала вдоль некоторого участка цепи или вдоль замкнутого контура. На графике по оси x откладывают величины сопротивлений вдоль контура, начав с условной токи, по оси y откладывают потенциалы. На потенциальной диаграмме каждой точке замкнутого контура или участка электрической цепи соответствует своя точка.
Рассмотрим пример того, как для контура abcea, изображённого на рисунке 1, можно построить потенциальную диаграмму.
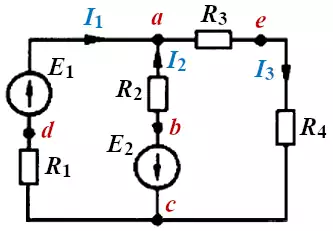
Рис. 1. Электрическая схема.
Пусть E1 = 80 В, E2 = 64 В, R1 = 6 Ом, R2 = 4 Ом, R3 = 3 Ом, R4 = 1 Ом, I1 = 14 А, I2 = -15А, I3 = -1А.
Суммарное сопротивление контура равно:
Rabcea = R2 + R3 + R4
Rabcea = 4 + 3 + 1 = 8 Ом
Чтобы построить потенциальную диаграмму, выберем масштабы для осей абсцисс и ординат.
Для любой из точек, например, точки a, примем потенциал, равный нулю: ϕa = 0. Данную точку поместим в самое начало координат.
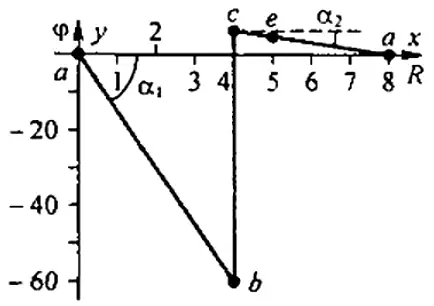
Рис. 2. Потенциальная диаграмма.
Определим потенциал точки b:
ϕb = ϕa + I2∙R2
ϕb = 0 + (-15∙4) = – 60 В
Координаты точки b: x = 4, y = -60.
Потенциал точки c:
ϕc = ϕb + E2
ϕc = -60 + 64 = 4 В
Координаты точки c: x = 4, y = 4.
Потенциал точки e:
ϕe = ϕc + I3∙R4
ϕe = 4 + (-1) ∙ 1 = 3 В
Координаты точки e: x = 5, y = 3.
Тангенс для угла α1 наклона прямой ab к оси x пропорционален электрическому току I2, тангенс угла α2 наклона прямой ce пропорционален электрическому току I3.
tgα = I ∙(mr / mϕ)
mr и mϕ – масштабы по осям x и y.
Стоит обратить внимание на имеющуюся разницу в знаках для падения напряжения IR в случае определения потенциала точки электрической схемы через потенциал изначальной точки и в случае составления уравнений в соответствии со 2-м законом Кирхгофа.
Энергетический баланс в электрических цепях постоянного тока
Когда по сопротивлению протекает электрический ток, в нём выделается тепло. По закону сохранения энергии тепло, которое выделяется в сопротивлениях электрической схемы в единицу времени, должно быть равно энергии, которая от источника питания доставляется за это же время.
Если направление протекающего через источник ЭДС тока I является совпадающим с направлением ЭДС, то в электрическую цепь источник ЭДС доставляет такую энергию в единицу времени (т.е. мощность), которая равняется E∙I. Данное произведение E∙I в составляемое уравнение энергетического баланса входит с положительным знаком.
В случае, если направление электрического тока I направлено против направления ЭДС E, то это означает, что источник ЭДС энергию не поставляет, а потребляет. Произведение E∙I входит в уравнение для энергетического баланса в этом случае с отрицательным знаком.
В случае питания исключительно от источника ЭДС, уравнение энергетического баланса будет таким:
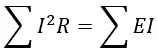
Когда питание электрической схемы происходит как от источника ЭДС, так и от источника тока, во время составления уравнений для энергетического баланса требуется учесть также энергию, которую даёт источник тока.
К примеру, если к узлу a течёт ток J от источника электрического тока, а от узла b данный электрический ток утекает, то мощность, которая доставляется источником тока будет равна UabJ.
Токи в ветвях схемы и напряжение Uab необходимо подсчитывать, учитывая ток, который течёт от источника тока. Это легче сделать, используя метод узловых потенциалов.
Уравнение энергетического баланса в общем виде: