 Выполним расчёт электрического поля плоской пластины бесконечных размеров, которая заряжена с постоянной плотностью. В основу положим закон Кулона для взаимодействия 2-х точечных электрических зарядов в вакууме. Если в какой-то точке пространства находится заряд Q, а на удалении R от него расположен некий пробный заряд q, то на данный пробный заряд в соответствии с формулой действует сила F.
Выполним расчёт электрического поля плоской пластины бесконечных размеров, которая заряжена с постоянной плотностью. В основу положим закон Кулона для взаимодействия 2-х точечных электрических зарядов в вакууме. Если в какой-то точке пространства находится заряд Q, а на удалении R от него расположен некий пробный заряд q, то на данный пробный заряд в соответствии с формулой действует сила F.

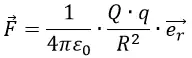
Где ε0 – диэлектрическая проницаемость вакуума;
R – расстояние между двумя зарядами Q и q;
Q и q – величины электрических зарядов;
er – единичный вектор, направленный по линии зарядов.
Если два электрических заряда Q и q помещены не в вакуум, в пространство с веществом, то к формуле добавляется относительная диэлектрическая проницаемость ε, которая отличает проводящие свойства какого-либо вещества от вакуума. ε является безразмерной константой.
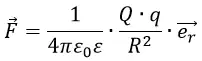
В данной формуле можно выделить часть, которая не зависит от пробного заряда q:
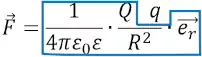
Обозначим её буквой E:
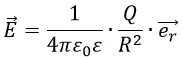
Она носит название «напряжённость электрического поля». Из определения следует, что напряжённость поля не зависит от величины пробного заряда q, помещённого в точку. Напряжённость электрического поля определяется однозначно исходным зарядом Q, а также расстоянием R до точки, то есть геометрией пространства.
В таком случае сила кулона F будет равна:
![]()
Эта формула применима для любого точечного заряда.
Электрическое поле обладает свойством суперпозиции. Если есть несколько электрических зарядов Q1 и Q2, то каждый заряд взаимодействует с точечными силами F1 и F2, и общая сила складывается по правилу сложения векторов.
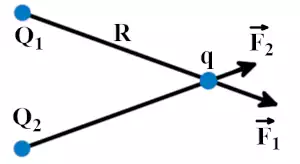
В такой ситуации можно написать:
![]()
F12 – суммарная сила.
Из формулы можно увидеть, что напряжённость электрического поля складывается. Этот факт называется принципом суперпозиции электрического поля, и он будет использован для расчёта сложной системы электрических зарядов, то есть зарядов, распределённых по плоскости.
Расчёт напряжённости электрического поля плоской пластины
Постановка задачи: имеется бесконечная плоская пластина с определённой плотностью заряда σ. Выделим на ней площадку dS. Заряд dQ площадки dS будет равен:
![]()
Будем считать, что плоская пластина равномерно заряжена и σ не зависит от координат.
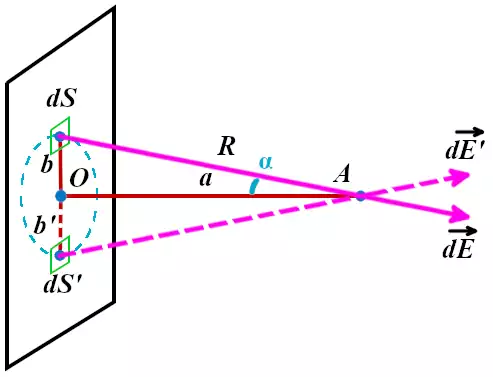
Посчитаем напряжённость электрического поля всей плоской пластины в точке A, находящейся на удалении a от этой пластины: E(A)=?
Для примера возьмём на плоской пластине небольшую площадку площадью dS на удалении b от центра. Обладая электрическим зарядом dQ, эта площадка создаёт электрическое поле с напряжённостью dE в точке A по закону Кулона.
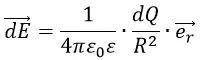
На расстоянии b‘, равному расстоянию b, будет находится площадка dS‘, которая будет создавать электрическое поле с напряжённостью dE‘, равное по величине напряжённости поля dE, но направленное под другим углом. При сложении двух этих полей сумма расположенных параллельно пластине составляющих их векторов будет равны нулю. В связи с этим нам нужно учитывать только составляющую, расположенную перпендикулярно поверхности плоской пластины.
Обозначим угол между напряжённостью поля dE и перпендикуляром к пластине через α. Тогда интересующая нас составляющая dE⊥ будет равна:
![]()
Точно такую же составляющую будут создавать все точки на плоской пластине, находящиеся на удалении b от точки O. Это связано с тем, что расстояния от них до точки A, а также углы между перпендикуляром и напряжённостями электрического поля будут такими же.
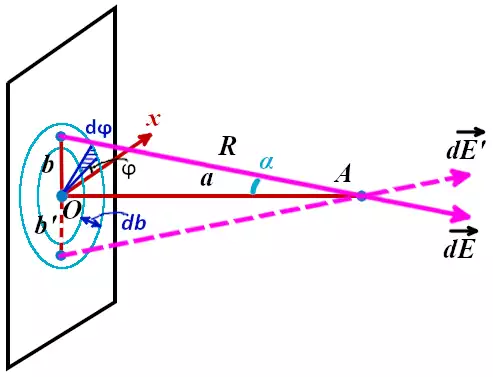
Выделим окружность радиусом b и толщиной db на плоской пластине. В полученном кольце рассмотрим элемент, расположенный под углом ϕ к оси x. Элемент вырезается из кольца в виде сегмента с размером dϕ. При малости dϕ и при малости db этот участок плоской пластины можно считать квадратом. В таком случае площадь dS будет равна:
![]()
Заряд dQ равен:
![]()
![]()
Полную напряжённость электрического поля кольца можно посчитать путём интегрирования по ϕ. А полное поле всей пластины можно посчитать путём интегрирования всех колец по b от 0 до ∞.
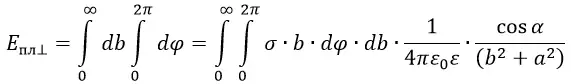
Для вычисления интеграла сделаем замену переменных и выразим всё через угол α. В этом случае получим:
![]()
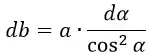
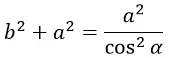
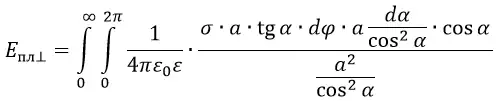
В данной формуле сокращаем cos2α и a. Интеграл от 0 до ∞ выразится в интеграл от 0 до π/2.
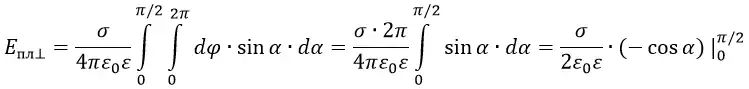
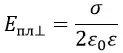
Физический смысл этой формулы состоит в том, что напряжённость электрического поля около равномерно заряженной плоской пластины не зависит от расстояния до этой пластины.