
Первый закон Кирхгофа для электрической цепи
Любые электрические цепи всегда подчиняются законам Кирхгофа.
Есть для первого закон Кирхгофа два варианта формулировок:
1. Алгебраическая сумма электрических токов ветвей, сходящихся в одном узле, равна нулю.
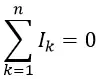
2. Сумма электрических токов, которые текут в направлении к узлу, равна сумме электрических токов, которые текут из узла.
Токи, направленные к узлам, обычно считают положительными, а выходящие – отрицательными.
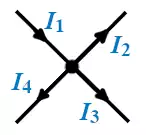
Рис. 1. Направление токов в узле.
Для рисунка 1 можно записать по первой формулировке:
![]()
По второй формулировке:
![]()
Физический смысл для первого закона заключается в том, что заряды в электрической цепи двигаются таким образом, что не скапливаются ни в каком узле.
Второй закон Кирхгофа для электрической цепи
Для второго закона тоже есть две формулировки:
1. В замкнутом контуре абсолютно любой электрической цепи алгебраическая сумма существующих падений напряжений равна сумме ЭДС контура.
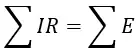
Если слагаемое совпадает с направление, по которому происходит обход контура цепи, то оно входит в уравнение со знаком «+», если же оно не совпадает – то со знаком «–».
2. Алгебраическая сумма напряжений вдоль какого-либо замкнутого контура цепи равна нулю.
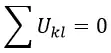
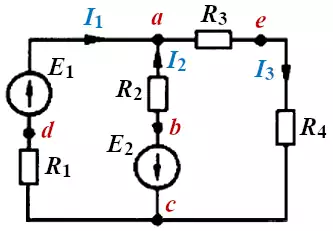
Рис. 2. Электрическая схема.
Для контура на рисунке 2 можно записать:
![]()
Оба закона Кирхгофа являются справедливыми как для линейных, так и для нелинейных электрических цепей при любых изменениях напряжений и токов во времени.
Метод составления уравнений по законам Кирхгофа
Оба закона Кирхгофа совместно применяют для поиска электрических токов в ветвях. Давайте обозначим число всех ветвей через b, число ветвей, где есть источник тока через bит, число узлов через y. По каждой из ветвей схемы протекает свой собственный электрический ток. По причине того, что токи, находящиеся в ветвях с источниками электрического тока, известны, число токов, которые неизвестны, равно b–bит.
Перед составление уравнения необходимо выбрать произвольно:
1. Положительное направление электрического тока в каждой из ветви, и затем обозначить их на схеме.
2. Положительные направления для обхода каждого из контуров схемы для записи уравнений по второму закону Кирхгофа.
Для удобства рекомендуется положительные направления для обхода каждого из контуров выбирать одинаковыми, допустим, по часовой стрелке.
С целью получения линейно независимых уравнений, которые были составлены по первому закону Кирхгофа, их количество должно быть равно y–1. Для последнего узла уравнение не составляют, потому что оно совпадало бы с уравнением, которое получено в результате суммирования уравнений для y–1 узлов.
В соответствии со вторым законом Кирхгофа выполняют составление уравнений в количестве, равном количеству ветвей без источника электрического тока (b–bит), вычтя те уравнения, которые были составлены по первому закону:
![]()
Во время составления уравнения по второму закону Кирхгофа, нужно охватить все ветви, при этом исключив ветви, где есть источник тока, потому что в этом случае в уравнение были бы включены бесконечно большие слагаемые, в связи с чем оно бы не имело смысла.
Есть рекомендуемое, но не обязательное требование, по которому при составлении в соответствии со 2-м законом Кирхгофа линейно независимых уравнений стремятся к тому, чтобы в каждый новый контур, применительно к которому выполняется составление уравнения, входила как минимум одна новая ветвь, которая не вошла в предыдущие контуры, для которых уравнения по 2-му закону уже составлены. Данные контуры называют независимыми контурами.
Анализ электрических цепей с помощью законов Кирхгофа
Произведём анализ электрических цепей для схемы, изображённой на рисунке 3 и составим для неё уравнения.
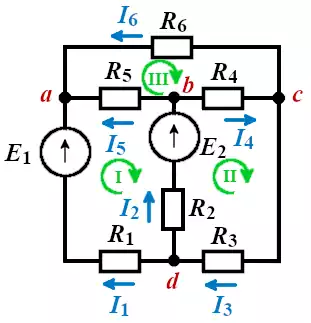
Рис. 3. Электрическая схема.
Число неизвестных электрических токов для схемы равно числу ветвей. Обозначим число ветвей через m, число узлов через k. Тогда m=6, k=4.
Теперь зададимся произвольным направлением электрических токов отдельных ветвей цепи. Согласно первого закона Кирхгофа составим независимые уравнения в количестве k–1 штук для узлов a, b и c.
a: I1 + I5 + I6 = 0
b: I2 – I5 – I4 = 0
c: I4 – I3 – I6 = 0
Для определения всех токов ветвей недостающие уравнения, количество которых (m–(k–1)), можно составить, если воспользоваться вторым законом для независимых контуров.
Контур I: I1R1 – I2R2 – I5R5 = E1 – E2
Контур II: I2R2 + I4R4 + I3R3 = E2
Контур III: I5R5 – I6R6 – I4R4 = 0