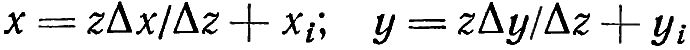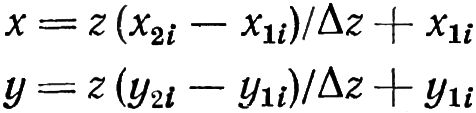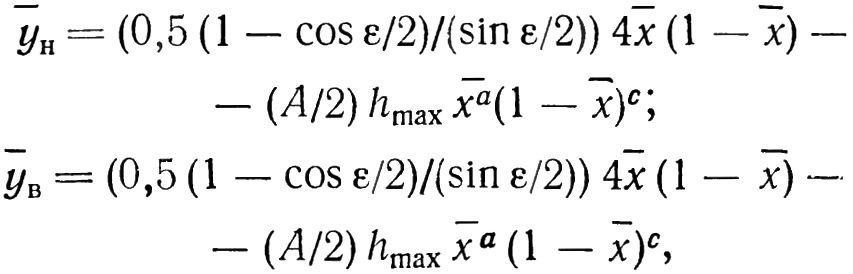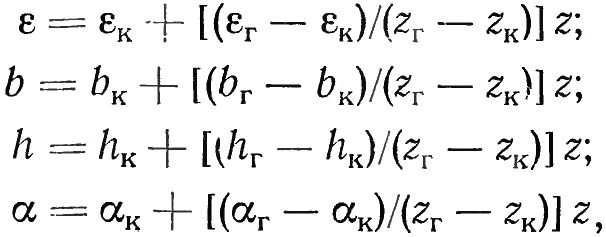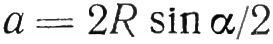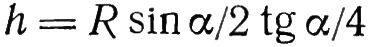Подготовка управляющих программ для механической обработки сложного профиля рабочих частей лопаток паровой турбины вручную очень сложна, а нередко и невозможна. Поэтому прилагаются усилия для создания систем автоматического программирования (САП). Необходимым условием успешного решения этой трудной задачи является отработка на технологичность конструкций рабочих частей лопаток, основу которой составляет математическое описание поверхностей.
Создаваемое для целей разработки системы автоматического программирования (САП) математическое описание поверхностей должно учитывать следующие факторы:
— требования по точности и шероховатости;
— технологический процесс обработки;
— емкость программы и массив промежуточных данных, и возможность размещения их в оперативной памяти ЭВМ;
— стыкуемость метода математического описания с машинными программами, используемыми для аэродинамического и прочностного расчетов.
По способу построения поверхности рабочей части лопаток газовых и паровых турбин и компрессоров можно разбить на два основных класса: аналитические и так называемые скульптурные.
Аналитические поверхности составлены из линейчатых, цилиндрических, конических, а также винтовых поверхностей.
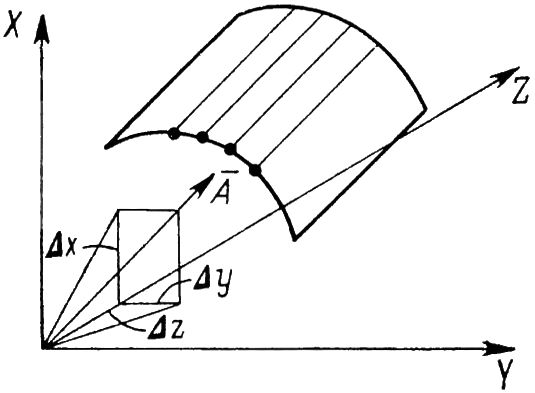
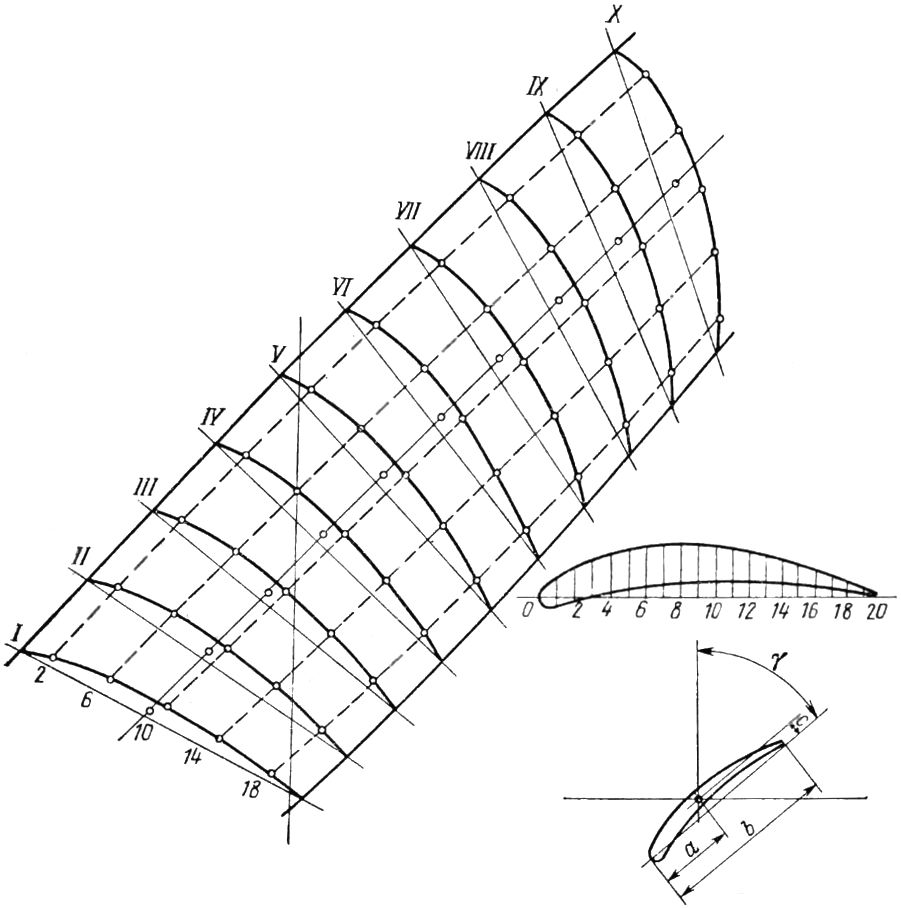
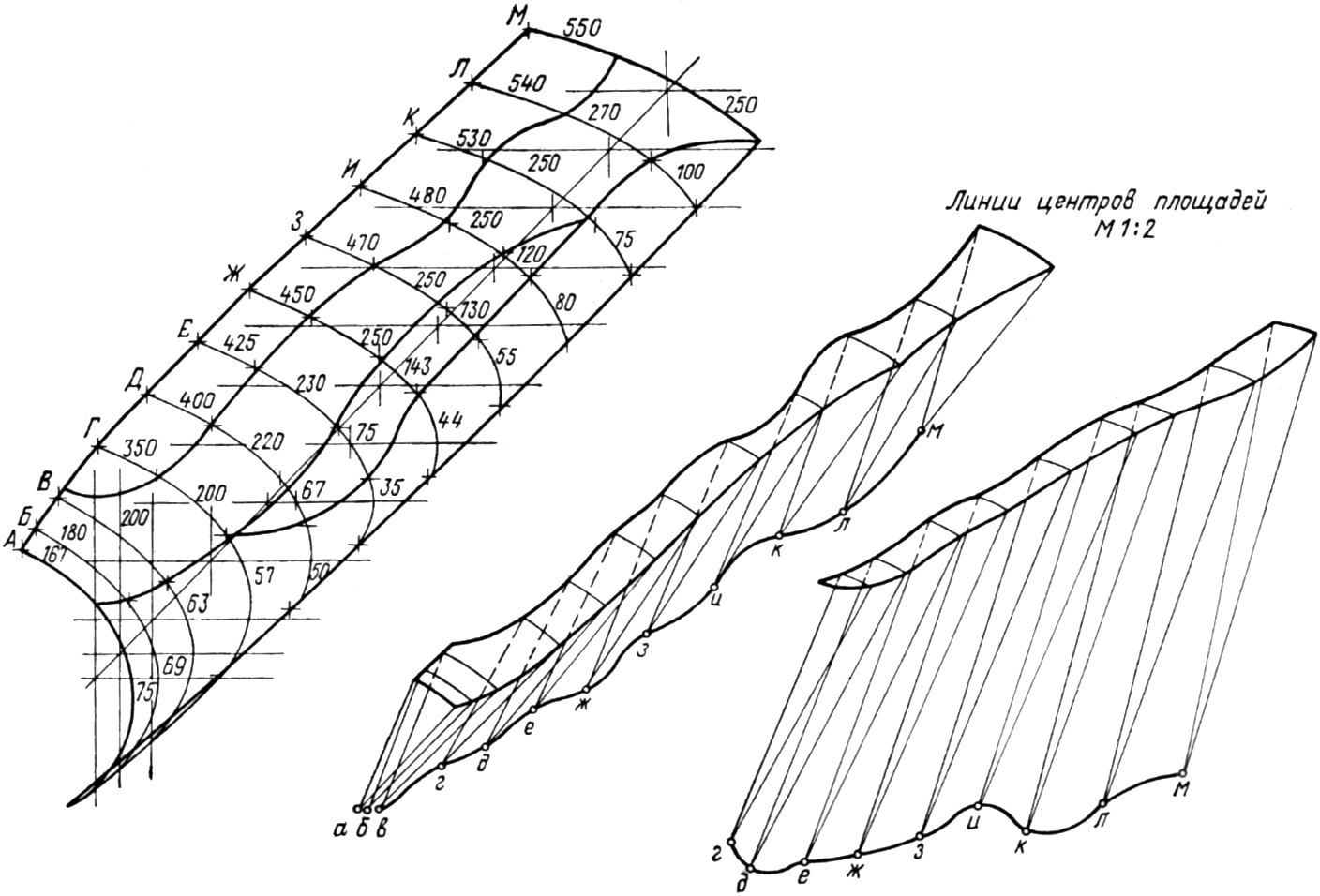
Изображенная на рис. 21.8 поверхность внутреннего профиля 18 ступени паровой турбины мощностью 200 МВт представляет собой цилиндрическую линейчатую поверхность. Ее поперечные сечения ограничены одними и теми же радиусами, а центры одноименных радиусов лежат на прямой линии, положение которой в пространстве определенно.
Рис. 21.8. Цилиндрическая линейчатая поверхность внутреннего профиля рабочей части лопатки паровой турбины: O1—O1 — линия центров радиуса R1; O2—O2 — линия центров радиуса R2.
Прямые линии, лежащие на образующей поверхности лопатки, параллельны направляющему вектору А (см. рис. 21.9). Уравнения этих прямых имеют вид:
Где отношения Δx/Δz и Δy/Δz постоянны для всех образующих линий. Координаты xi и yi определяются по данным чертежа корневого сечения лопатки.
Рис. 21.9. Графическое построение к уравнениям образующих прямых линейчатых цилиндрических поверхностей.
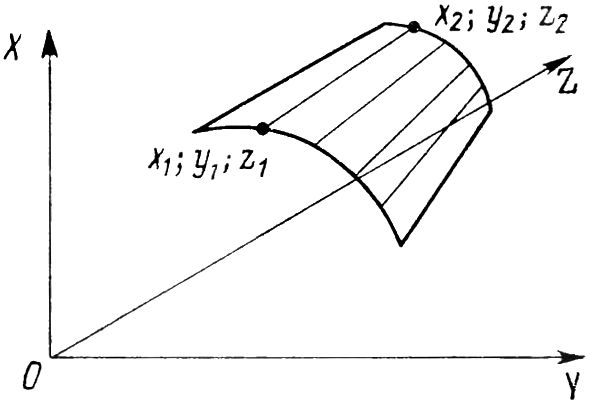
На рис. 21.10 приведено графическое построение, поясняющее уравнения образующих прямых конических линейных поверхностей.
Рис. 21.10. Графическое построение к уравнениям образующих прямых линейчатых конических поверхностей.
Уравнения имеют вид:
Где координаты x1i, x2i, y1i и y2i, определяемые по данным чертежа корневого и головного сечений.
У винтовых поверхностей деталей паровой турбины контур корневого сечения не только перемещается вдоль косо расположенной прямой линии, но и поворачивается вокруг нее. Образованная подобным образом поверхность представляет собой геликоид переменного шага. Указанная поверхность может быть представлена математически в форме, удобной для обработки на ЭВМ.
Координаты точек профиля вдоль всей лопатки турбины определяются формулами:
Где ε — угол изгиба дужки (центральный угол); A, a, c — постоянные; hmax — толщина сечения в зените; x = x/b — абсцисса; b — величина хорды (рис. 21.11).
Рис. 21.11. Графическое построение к формулам расчета координат точек профиля винтовой поверхности.
В общем случае величины ε, hmax, b и α переменные вдоль лопатки паровой турбины. Закон их изменений в функции известен и чаще всего линеен:
Где εк, bк, hк, αк — параметры корневого сечения; εг, bг, hг, αг — параметры головного сечения.
Семейство приведенных уравнений полностью определяет поверхность лопатки. Варьируя коэффициенты A, a, c можно получать профили различной формы.
Некоторые лопатки турбин существующих конструкций, хотя и заданные в чертежах табличным методом, размеры в которых определяют сечения и их положение вдоль оси, но они в то же время поддаются и приведенному выше математическому описанию. К таким относятся рабочие и направляющие лопатки энергетических газотурбинных установок (ГТУ) моделей ГТ-100-750, ГТУ-60. Кроме того, при отработке конструкций на технологичность удовлетворительные результаты дала аппроксимация с помощью приведенных формул поверхностей лопаток газотурбинной установки ГТН-9, лопаток некоторых ступеней установки ГТН-10, компрессора высокого давления установки ГТ-25.
Если вне зависимости от метода задания поверхностей лопатки на чертеже они могут быть заданы аналитически, то в каком-либо новом виде описания указанные поверхности не нуждаются, и управляющие программы для их обработки на станках с ЧПУ могут быть получены на ЭВМ с применением разрабатываемой системы автоматического программирования (САП).
Скульптурные поверхности характерны для значительного числа, как правило, и наиболее трудоемких при подготовке производства и в изготовлении лопаток турбин переменного профиля.
Условное название поверхности «скульптурная» хорошо отражает технологический прием ее формирования. Сечения припассовываются к шаблонам, а между сечениями поверхность доводится под контролем визуального чувства гладкости.
Различают два способа задания скульптурных поверхностей: с числовыми отметками, радиусографическим построением.
На рис. 21.12 наружный профиль рабочей части лопатки турбин задан способом с числовыми отметками. Контрольные сечения лопатки определяются координатами точек.
Рис. 21.12. Наружный профиль рабочей части лопатки 2-й ступени компрессора низкого давления энергетической газотурбинной установки ГТ-100-750.
Скульптурные поверхности с числовыми отметками нуждаются в математическом описании в целях интерполяции участков между точками, которые заданы чертежом, и получения при этом остальных опорных точек сколько того требует точность и класс шероховатости обработки. Для интерполяции необходимо использовать нелинейные функции, так как в противном случае контур будет представлять ломаную линию. Это замечание относится как к поперечным, так и продольным линиям.
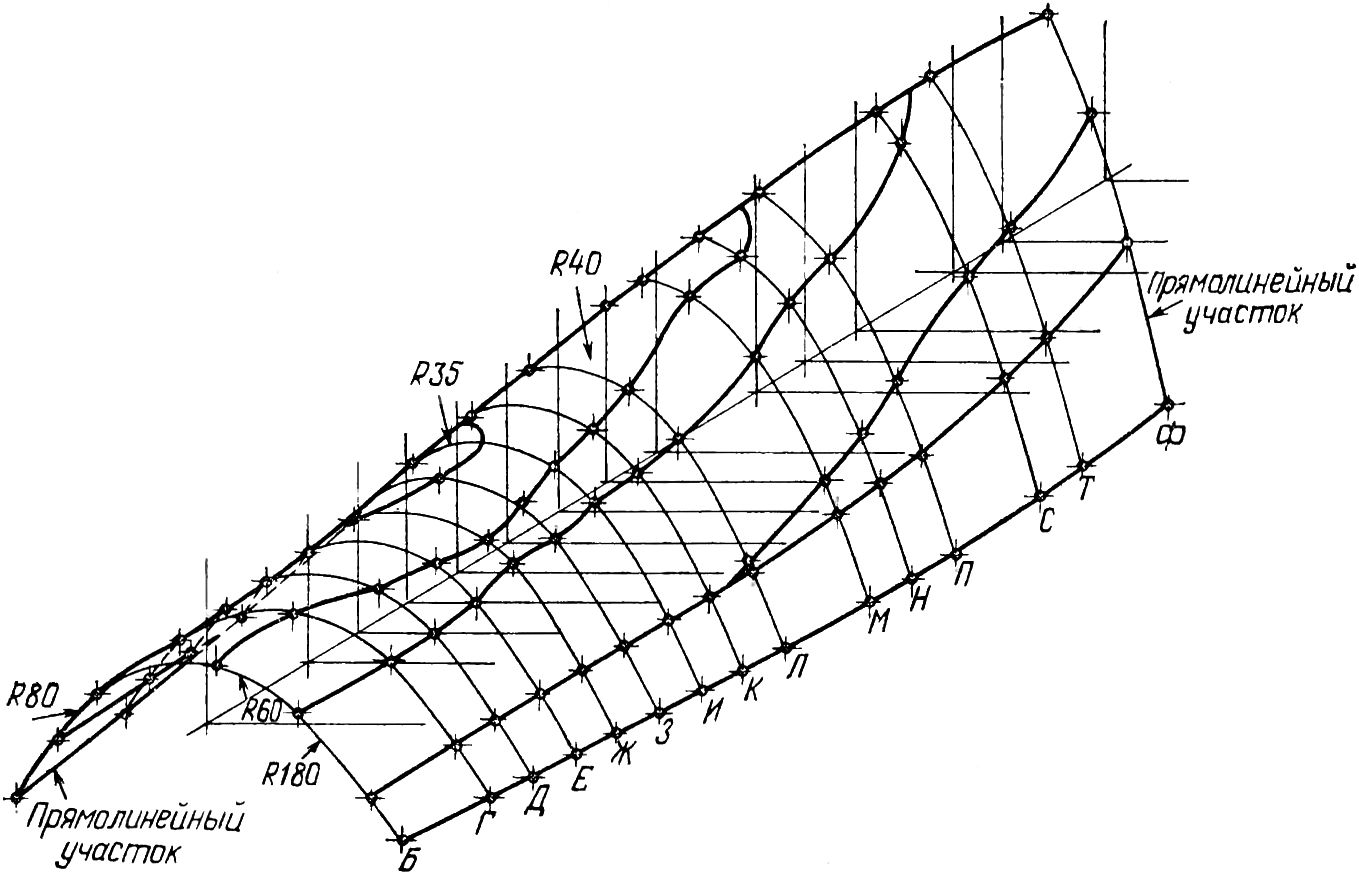
Поверхность рабочей части лопатки паровых турбин при радиусографическом способе построения (рис. 21.13) составлена из ряда зон, каждая из которых образована своим радиусом. Зона представляет собой участок цилиндрической поверхности с искривленной осью.
Рис. 21.13. Радиусографическое построение наружной поверхности рабочей части лопатки 29-й ступени паровой турбины К-300-240.
Наружная поверхность (рис. 21.14) рабочей лопатки 3-й ступени турбины низкого давления энергетической газотурбинной установки ГТ-100-750 задана поперечными сечениями, образованными переменными по величине радиусами. Причем центры этих радиусов лежат на пространственной кривой с незаданным законом построения.
Рис. 21.14. Построение наружной поверхности рабочей части лопатки 3-й ступени турбины низкого давления энергетической газотурбинной установки ГТ-100-750.
Скульптурные поверхности радиусографического построения требуют математического описания прежде всего с целью выявить геометрическую закономерность вдоль лопатки. В заданных сечениях контуры определены чертежом полностью и их можно было бы сохранить, если бы они хорошо согласовывались между собой единым продольным описанием поверхностей. Но, как показывает практика, контуры радиусографического построения плохо согласовываются между собой, а поэтому необходимо их переописание.
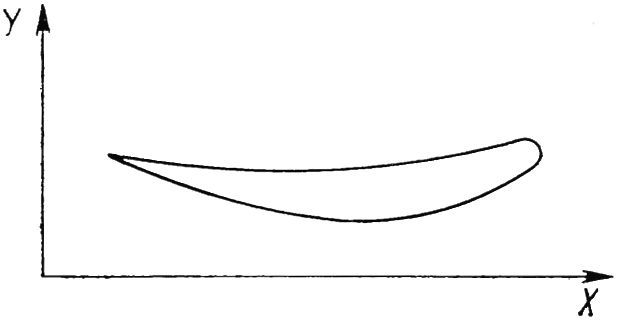
На рис. 21.15 приведено поперечное сечение рабочей части турбинной лопатки. В принятой системе координат ось X направлена от входной кромки к выходной кромке, а ось Y — от наружного профиля к внутреннему профилю. В выбранной системе и внутренний и наружный профили в подавляющем большинстве случаев выпуклые в отрицательном направлении оси Y. Угол между касательной к профилю и осью X в точке сопряжения с выходной кромкой всегда острый, т. е. никогда не превышает 90°. Аналогичный угол на входной кромке также остается всегда острым, а в головных сечениях может менять знак на противоположный. Таким образом, угол между крайними касательными у профилей постоянного знака кривизны никогда не превышает 180°.
Рис. 21.15. Поперечное сечение рабочей части лопатки паровой турбины.
В контурах радиусографического построения кромочная дуга четко определена координатами точек сопряжения и радиусом. В контурах, заданных числовыми отметками, границы кромки чертежом не определены, и кромочная зона отличается лишь густотой точек. В этом случае отнесение пограничного участка к кромке или к профилю может быть подчинено требованиям математического описания.
Характерной особенностью профилей лопаток последних ступеней паровых турбин являются прямые участки контура, сопрягающиеся с кромочным радиусом, т. е. с переходом от участков с конечным значением радиуса к участкам с бесконечным значением радиуса. Характерно также наличие в данных чертежа погрешностей. В частности, встречается несопряжение участков, формирующих контур поперечного сечения, образующих ступеньки из-за смещения соседних участков или переломы из-за несовпадения касательных к соседним участкам в точке сопряжения.
Плавность продольных образующих обычно контролировалась только графическим построением с неизбежными для этого метода неточностями. Вследствие этого не удается построить какую-либо образующую аналитическим интерполяционным методом так, чтобы она проходила через все заданные чертежом контуры и в то время не меняла знака кривизны. Постоянство знака кривизны может быть достигнуто либо аппроксимацией, т. е. в той или иной степени отходом от заданных контуров, либо коррекцией положения профиля.
В существующих конструкциях лопаток паровой турбины достаточно строго оговаривается только требование к контрольным профилям радиусографического построения. Весь контур при этом задан непрерывно, указано допустимое отклонение от формы и толщины профиля. Возможное изменение положения поверхности ограничивается указанием в чертеже допустимого смещения профилей в направлении, перпендикулярном оси лопатки и тем самым оговаривается допустимое искривление поверхности вдоль лопатки. Кроме того, имеется абсолютно нестрогое указание о допустимом отклонении со значением 0,1—0,15 мм продольных образующих от прямых линий на участках между соседними сечениями. При этом направление образующей не указывается. В профилях заданных таблично, не указывается вид кривой, соединяющей точки. Радиусографическое построение содержит резкие перепады радиусов, т. е. кривизна имеет разрывы.
Математическое описание, выполняемое при отработке на технологичность конструкций рабочих частей турбинных лопаток, должно исключать приведенные и другие невязки задания поверхностей. При этом должны быть соблюдены следующие положения.
Поверхность не должна иметь локальных выступов и впадин. Это выполнимо при условии, что образующие линии — линии продольного каркаса — либо вообще не меняют знака кривизны, либо меняют его в том месте, где это предусмотрено конструкцией турбинной лопатки. Возможны смещения внутренних и наружных профилей в пределах допуска на толщину, а также коррекция формы профиля в пределах 0,3—0,5 мм.
Существует несколько методов математического описания поверхностей лопаток. Ленинградский институт авиационного приборостроения (ЛИАП) и ВПТИэнергомаш разработали метод математического описания поверхностей лопаток стационарных паровых турбин и газотурбинных установок. Как отмечают авторы, наибольшую трудность в рассматриваемой задаче представляет построение образующих линий — линий продольного каркаса. Здесь важно выбрать семейство таких линий, которые наилучшим образом представляли бы поверхность. Это значит, что они могли бы быть проконтролированы и на них можно было бы перенести технические требования чертежа. К таким относятся эквинормальные линии, т. е. линии, соединяющие точки контрольных сечений с одинаково направленными нормалями, восстановленными из этих точек по отношению к контуру поперечного сечения. Указанные линии в применении к математическому описанию поверхностей турбинных лопаток имеют ряд конкретных преимуществ. Эти линии наиболее пологие и однородные по своей геометрии из всех линий, которые можно провести на поверхности, а это облегчает их аппроксимацию. Направление нормали к этой линии постоянно по всей ее длине, что облегчает вычисление эквидистантной траектории.
Распределение частоты эквинормальных линий поперек поверхности можно подчинить самым различным требованиям, для чего необходимо знать действующие при этом соотношения. Так, длина хорды, стягивающей дугу поперечного контура между двумя соседними линиями, определяется простым равенством:
Где R — радиус кривизны дуги; α — угол между направлениями нормалей соседних линий.
Высота сегмента, характеризующая погрешность линейной интерполяции, определяется выражением:
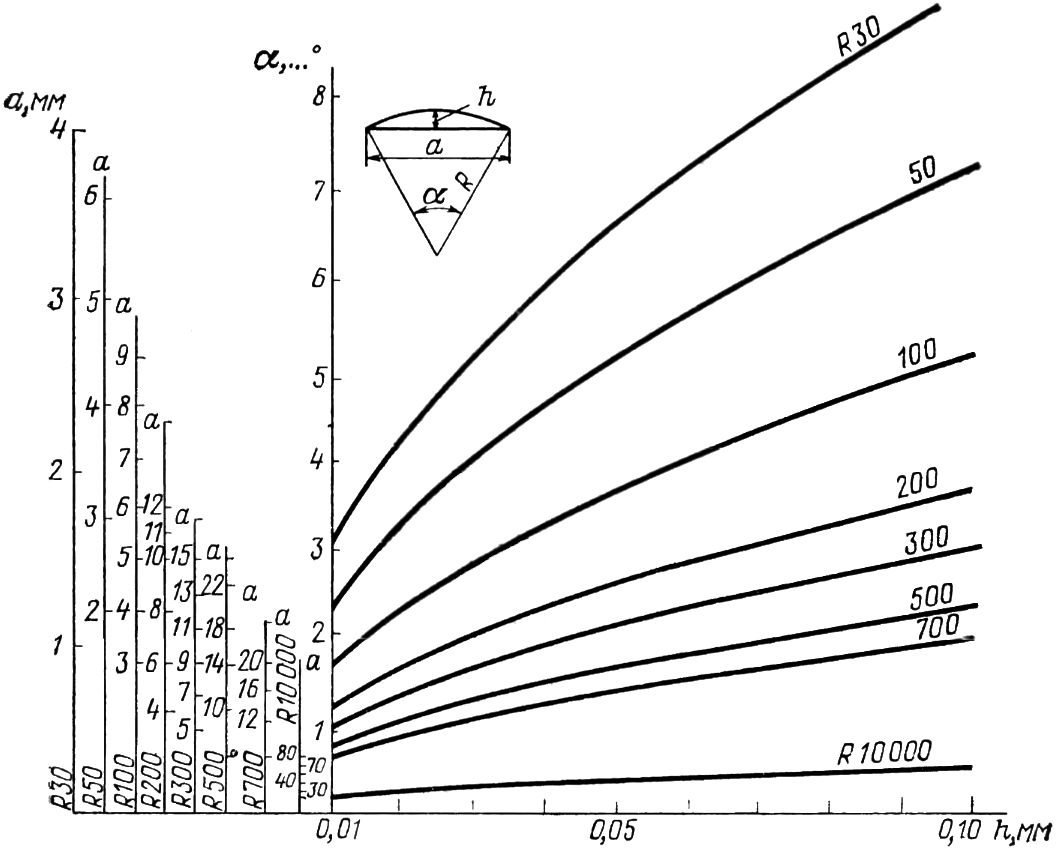
Соотношение между погрешностью h интерполяции, шагом а интерполяции, угловым шагом α интерполяции и характерными для лопаток турбин величинами радиусов R кривизны представлены графически на рис. 21.16. Радиус R = 10 000 мм приведен в связи с тем, что он используется при замене прямых участков.
Рис. 21.16. Зависимость величин, характеризующих сечение лопатки паровой турбины.
Вышеизложенное является первой отличительной особенностью метода математического описания поверхностей лопаток.
Вторая особенность связана со способом аппроксимации кромочной линии. Трудоемкость этой задачи заключается в большом количестве накладываемых условий, так как требуется обеспечить сопряжение с наружным и внутренним профилем в точках, заранее неизвестных, касание к прямой, ограничивающей ширину контура, и близость контура кромки к окружности.
Задача вписывания окружности между прямой и двумя кривыми второго порядка не имеет прямого аналитического решения. Поэтому осуществляется поэтапное решение. Сначала окружность вписывается между прямой и двумя касательными к кривым второго порядка. Ближайшие к окружности точки на наружном и внутреннем профиле принимаются за точки сопряжения, и затем уже кромка интерполируется двумя участками кривых второго порядка.
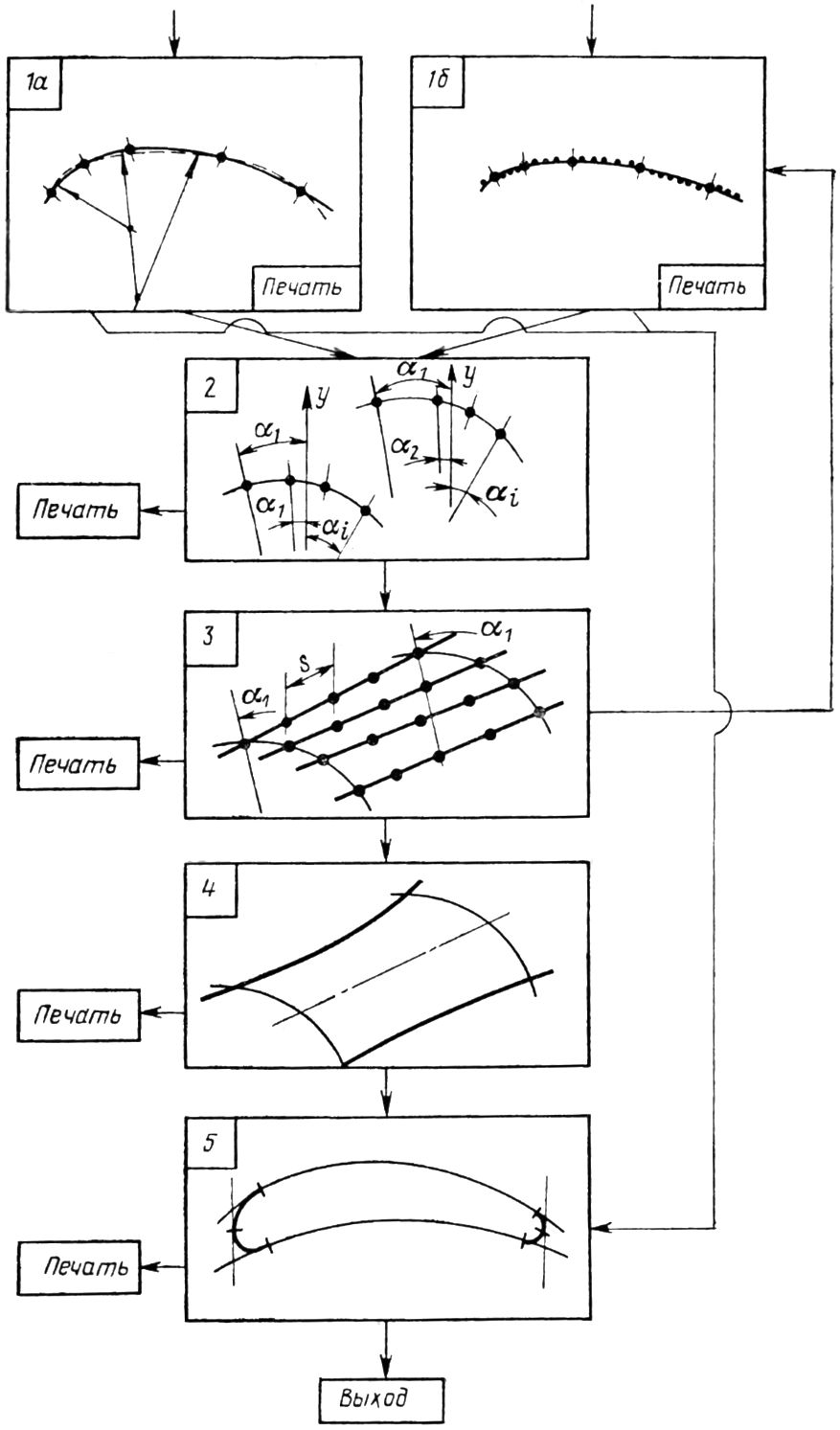
На рис. 21.17 приведено разграничение алгоритма решения задачи по методу ЛИАП — ВПТИэнергомаш на пять основных частей. В первой части производится аппроксимация поперечных сечений лопатки кривыми второго порядка и вычисление величины погрешности аппроксимации. Во второй части формируются исходные данные для построения продольного каркаса турбинной лопатки эквинормальными линиями. Третья часть алгоритма предусматривает построение эквинормальных линий и расчет исходных данных для промежуточных сечений. В четвертой части производится построение линий, ограничивающих габарит лопатки по кромкам. В пятой части формируются контуры кромок.
Рис. 21.17. Состав алгоритма математического описания поверхности лопатки паровой турбины.
На рисунке через α обозначена задаваемая в градусах величина шага между продольными каркасными линиями, а символом s — шаг промежуточных сечений.
Если определенная расчетом на ЭВМ поверхность лопатки паровой турбины отличается от заданной чертежом на величины, не превышающие допустимых, то отработка ее конструкции на технологичность заключается в переоформлении чертежа. В тех случаях, когда полученные расчетом задающие поверхность параметры превышают наперед заданные отклонения, то решение о корректировании чертежа рабочей части лопатки принимается после прочностной и аэродинамической оценок.
В результате расчета получают входные данные для управляющей программы к станку с ЧПУ для обработки профиля лопатки турбины.
- Технологичность конструкций деталей, улучшающая условия обработки на станках с ЧПУ
- Технологичность конструкций деталей, улучшающая программирование станков ЧПУ