Под напряжение на участке электрической цепи имеется ввиду разность потенциалов на крайних точках участка.
Определение напряжения на участке электрической цепи без ЭДС
На рисунке 1 показан участок цепи, где крайние точки обозначены при помощи букв a и b. Постоянный электрический ток I протекает к точке b от точки a, где точке a соответствует более высокий потенциал ϕa, а точке b более низкий потенциал ϕb. Потенциал ϕa можно определить по формуле:
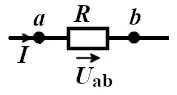
Рис. 1. Участок цепи без ЭДС.
Напряжение между этими точками:
В итоге мы имеем:
Разность потенциалов, присутствующую на концах сопротивления, обычно называют падением напряжения на сопротивлении.
Указываемое на рисунках при помощи стрелки положительное направление падения напряжения на участке электрической цепи, то есть направление отсчёта напряжения, совпадает с положительным направление для отсчёта электрического тока, который течёт по сопротивлению.
При этом положительное направление для отсчёта тока является совпадающим с положительным направление для нормали к поперечному сечению проводника в случае определения электрического тока по формуле:
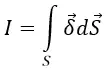
dS – элемент площади поперечного сечения;
δ – плотность электрического тока.
Определение напряжения на участке электрической цепи, содержащем ЭДС
На рисунках 2 и 3 можно увидеть участки цепей, где протекает постоянный электрический ток I. Определим напряжение (разность потенциалов) между точками a и c.
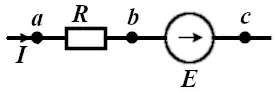
Рис. 2. Участок цепи, содержащей ЭДС. Перемещение против ЭДС.
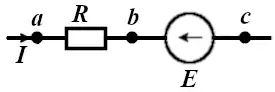
Рис. 3. Участок цепи, содержащей ЭДС. Перемещение согласно ЭДС.
Попробуем выразить через потенциал тоски c потенциал точки a. Для случая на рисунке 2, перемещение к точке b от точки c происходит встречно ЭДС, и потенциал на точке b меньше, чем на точке c на величину ЭДС:
Для случая на рисунке 3, перемещение к точке b от точки c происходит согласно с ЭДС и потенциал на точке b больше, чем на точке c на величину ЭДС:
По причине того, что электрический ток течёт к более низкому потенциалу от более высокого по участку электрической цепи, где нет источника ЭДС, потенциал для точки a получается больше, чем потенциал точки b, на величину, равную падению напряжения на сопротивлении:
Для рисунка 2 мы имеем:
Для рисунка 3 мы имеем:
В случае положительного направления для напряжения Uac, его показывают стрелкой, направленной от точки a к c. Так как Uca=ϕc–ϕa, то Uca=–Uac. Иными словами, смена чередования индексов соответствует изменению знака напряжения. Само напряжение может быть как положительным, так и отрицательным.
Закон Ома для участка цепи без ЭДС
Закон Ома для участка цепи без ЭДС показывает связь между напряжением и постоянным током на данном участке.
Для рисунка 1:
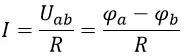
Закон Ома для участка цепи, содержащего ЭДС
Закон Ома для участка цепи, содержащего ЭДС, даёт возможность найти электрический ток на этом участке, используя разность потенциалов на концах участка ϕc–ϕc и ЭДС этого участка.
Для рисунка 2:
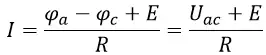
Для рисунка 3:
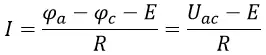
Для общего случая:
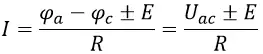
Последнее уравнение выражает математически закон Ома для участка цепи с ЭДС, при этом знак плюс соответствует ситуации на рисунке 2, знак минус – на рисунке 3.