Механическая характеристика асинхронного двигателя

Механической характеристикой называется зависимость скорости асинхронного двигателя от момента на его валу.

Выражение механической характеристики можно получить из выражения потерь для асинхронного двигателя.

Δp₂ = P_эм – P₂ = M·ω₀ – M·ω = M·(ω₀ – ω) = M·ω₀·s

P_эм – электромагнитная мощность – мощность, передаваемая через воздушный зазор из статора двигателя в ротор. Она может быть электрической и механической.

P₂ – полезная мощность, может быть только механическая, и равна произведению момента на валу двигателя на его скорость.

ω₀ – ω₀·(1 – s) = ω₀ – ω₀ + ω₀·s

Δp₂ = 3·(I₂’)²·r₂’

3·(I₂’)²·r₂’ = M·ω₀·s

Упрощенная формула механической характеристики асинхронного двигателя:

M = [3·(I₂’)²·r₂’] / [ω₀·s] (1)

Подставим в формулу (1) значения тока I₂’, определенного по схеме замещения.

Выражение полной формулы механической характеристики:

M = [3·U_ф²·(r₂’/s)] / [ω₀·[(r₁ + r₂’/s)² + x_к²]] (2)

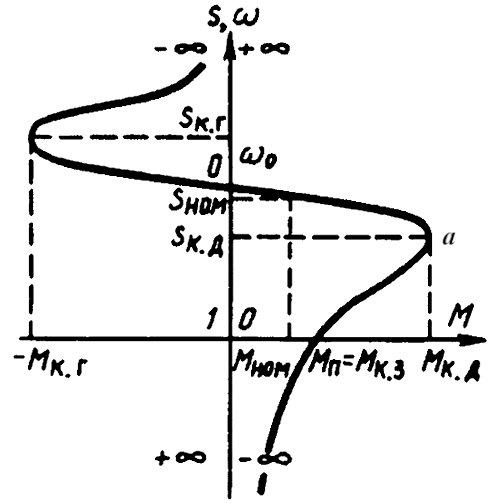
Если в формулу (2) подставить s от 0 до ±∞, то получится механическая характеристика асинхронного двигателя.

Механическая характеристика асинхронного двигателя.

Как видно из механической характеристики, она имеет два экстремума: первый в области положительных скольжений, второй в области отрицательных скольжений.

dM/ds = 0, можно определить максимальное значение момента, которое называют критическим моментом.

M_max = M_кр = [3·U_ф²] / [2·ω₀·(r₁ ± √(r₁² + x_к²))] (3)

s_кр = ±(r₂’/x_к) (4)

Как видно из формулы (3), момент критический будет иметь разные значения, в области скольжений больше нуля будет знак «+», в области скольжений меньше нуля будет знак «–».

Величина критического скольжения одинаковая и в двигательном и в генераторном режимах, только имеет разные знаки.

Если выражение (1) разделить на выражение (2), можно получить, так называемую, формулу Клосса:

M = [2·M_к·(1 + a·s_кр)] / [s/s_кр + s_кр/s + 2·a·s_кр] (5)

a – это коэффициент.

a = r₁/r₂’

Обычно у асинхронных двигателей активное сопротивление статора r₁ на порядок меньше активного сопротивления ротора r₂’, поэтому с достаточной степенью точности можно записать, что r₁=0, и тогда a=0.

M = [2·M_к] / [s/s_кр + s_кр/s] (6)

Если (5) называется полной формулой Клосса, то (6) называется упрощенной формулой Клосса.

Упрощенная формула критического момента:

M_кр = [3·U_ф²] / [2·ω₀·x_кр]

В двигательном режиме скольжение изменяется от 1 до 0.

Рассмотрим анализ формулы Клосса для двигательного режима работы. Как видно из характеристики, ее можно разбить на два участка: s > s_кр и s < s_кр.

Рассмотрим участок s > s_кр, тогда отношением s_кр/s можно пренебречь:

M = 2·M_к· s_кр / s = A/s

Как видно из получившейся формулы, связь между моментом и скольжением носит гиперболический характер. Это нелинейная не рабочая часть механической характеристики.

Рассмотрим участок s < s_кр, тогда отношением s/s_кр можно пренебречь:

M = 2·M_к·s / s_кр = B·s

На участке s < s_кр связь между моментом и скольжением линейная.

Из анализа формулы Клосса видно, что механическая характеристика имеет два участка: линейный рабочий и нелинейный нерабочий.

Для того чтобы определить характеристику двигателя в генераторном режиме, которая имеет также два участка: линейный и нелинейный, достаточно знать значение критического момента в генераторном режиме. Нелинейная область в генераторном режиме не может быть использована из-за больших значений токов и моментов.

λ = M_кр.д./M_н

Критический момент можно определить для двигательного режима по паспортным данным, в них задается отношение M_кр.д./M_н.

M_кр.г. = M_кр.д. · [r₁ + √(r₁² + x_к²)] / [r₁ – √(r₁² + x_к²)]

• Схема включения и электромеханическая характеристика асинхронного двигателя

https://iwantconcept.store ассиметричная юбка женская купить.