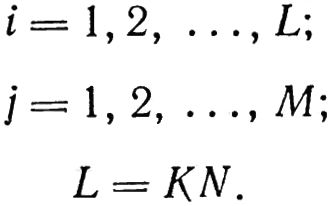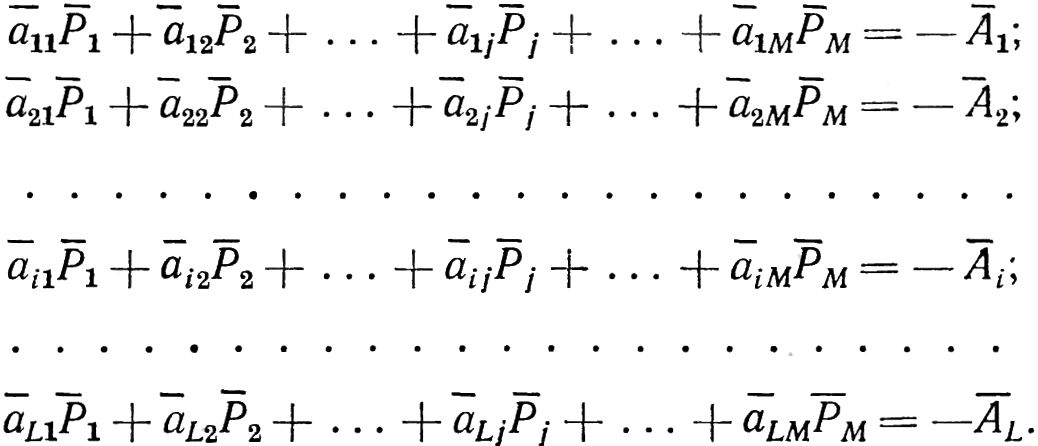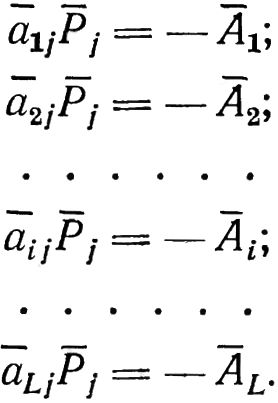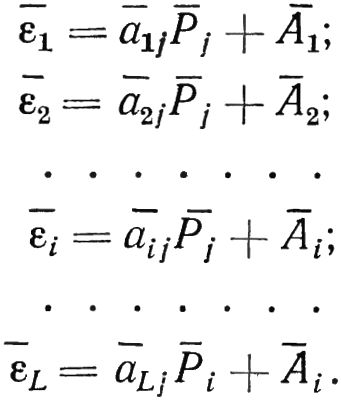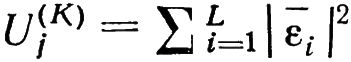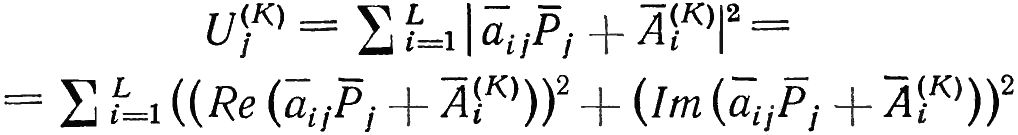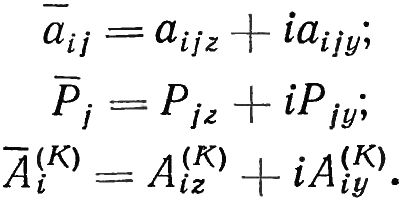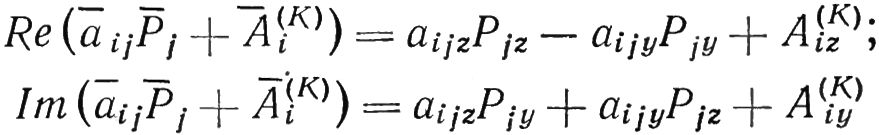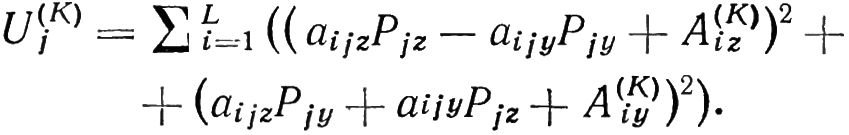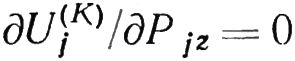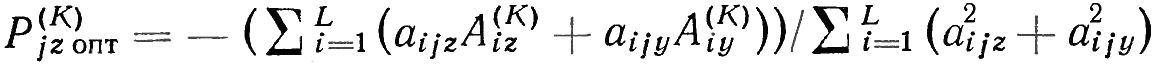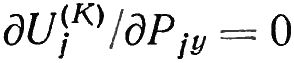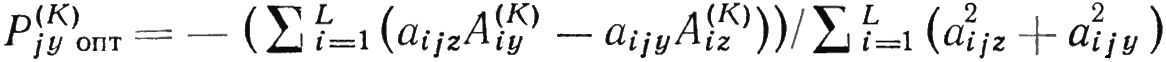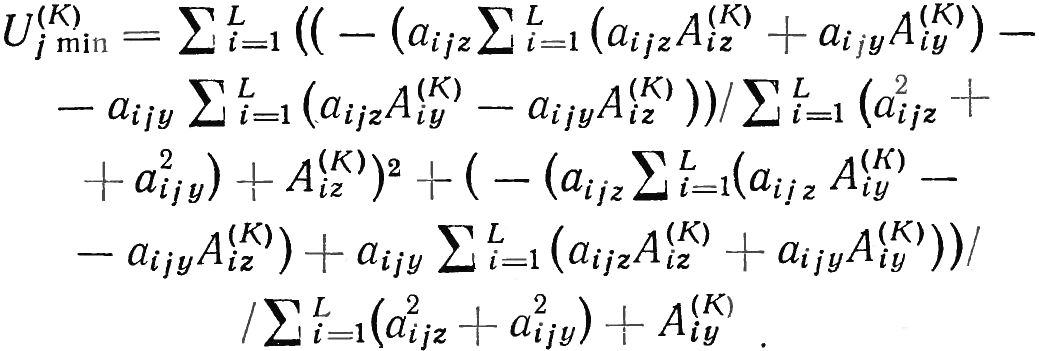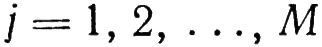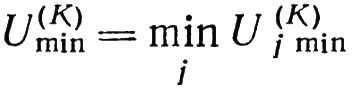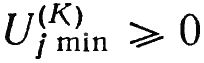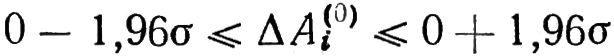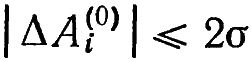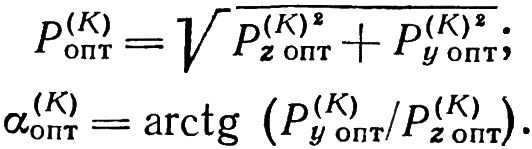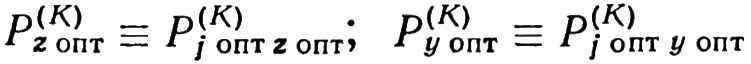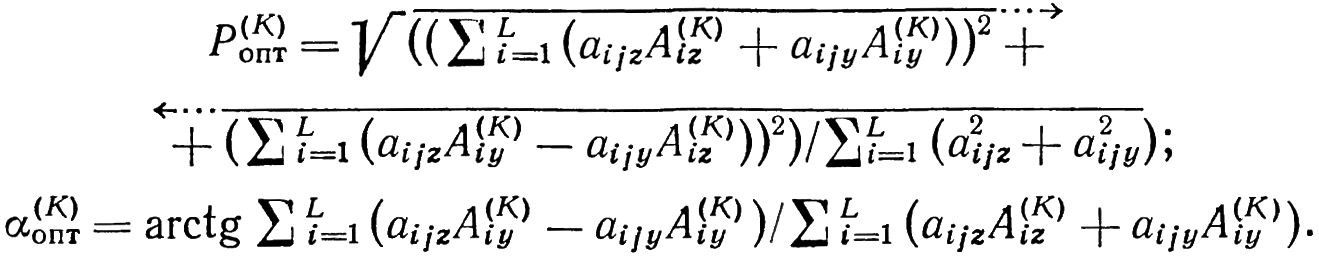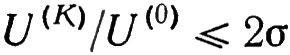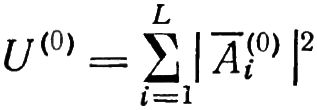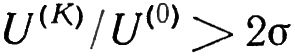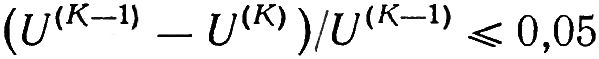Сущность метода заключается в следующем. Плоскости коррекции определяются при конструировании ротора паровой турбины. На балансировочном станке определяются начальные виброскорости каждой из опор. Критерием качества балансировки принимается минимум суммы квадратов амплитуд (модулей) остаточных виброскоростей. Тогда задача оптимальной балансировки ротора турбины формулируется следующим образом.
Для выбранной плоскости j коррекций найти такие величину и положение корректирующего груза Pj чтобы сумма квадратов амплитуд остаточных виброскоростей приняла наименьшее значение, т. е. пусть Uj=Uj(Pj) — сумма квадратов амплитуд остаточных виброскоростей, где Pj — комплексный вектор корректирующего груза.
По принятому в теории оптимального управления определению Uj = Uj(Pj) является функционалом (критерием качества балансировки) на множестве векторов {Pj}. Тогда задача состоит в том, чтобы найти оптимальный вектор Pj опт такой, который доставит функционалу Uj минимум, т. е.:
Uj (Pj) → min.
Рассмотренный вычислительный процесс итерационный. Все указанные действия повторяются для j = 1, 2, …, M, и затем из всех локальных минимумов Uj min выбирается наименьший, глобальный минимум Umin.
Далее рассчитывается оптимальный корректирующий груз Pkопт где k — номер итерации. Остаточные виброскорости Āi (i = 1, 2, …, L), которые одновременно являются начальными виброскоростями для следующего шага итерации, который выполняется аналогично предыдущему.
Процесс должен продолжаться до тех пор, пока отношение суммы квадратов остаточных виброскоростей к сумме квадратов начальных виброскоростей не станет меньше или равно средней квадратичной относительной погрешности измерения. Если относительное уменьшение суммы квадратов остаточных виброскоростей на двух последующих шагах не превышает 5%, то процесс итерации прекращается.
Выведем необходимые расчетные формулы. Для этого рассмотрим исходную систему уравнений расчета корректирующих грузов, приведенную для расчета коэффициентов чувствительности по методу наименьших квадратов.
Для упрощения последующих выкладок переобозначим индексы величин, входящих в систему.
Обозначим: i — номер строки (номер замера виброскорости); j — номер столбца (номер плоскости коррекции), где:
Тогда упомянутая исходная система примет вид:
В соответствии с общим планом рассчитываем оптимальные корректирующие грузы поочередно в каждой из M плоскостей коррекции.
Рассмотрим произвольную j-ю плоскость коррекции. В этом случае рассчитываем корректирующий груз Рj только для этой плоскости и, следовательно, считаем, что во всех остальных M — 1 плоскостях корректирующие грузы отсутствуют. Тогда в исходной системе останется лишь j-й столбец:
Очевидно, что при i > 1 полученная система уравнений переопределена и при линейно независимых уравнениях несовместна. Следовательно, как указывалось ранее, ее точного решения несуществует. Пользуясь обозначениями компонентов вектора Е невязки, имеем:
Компоненты вектора невязки по физическому смыслу представляют собой остаточные виброскорости.
Все величины, входящие в рассмотренные уравнения, являются комплексными амплитудами установившихся колебательных процессов. Следовательно, понятие истинной амплитуды этих процессов совпадает с понятием модуля их комплексной амплитуды. Поэтому критерий качества балансировки — функционал Uj является в то же время суммой квадратов модулей остаточных виброскоростей:
Подставим в полученную формулу значения εi, из последней системы уравнений:
Где Re — обозначение вещественной части комплексной величины; Im — обозначение мнимой части комплексной величины; Ai(K) — комплексные векторы начальных виброскоростей на K-м шаге итерации.
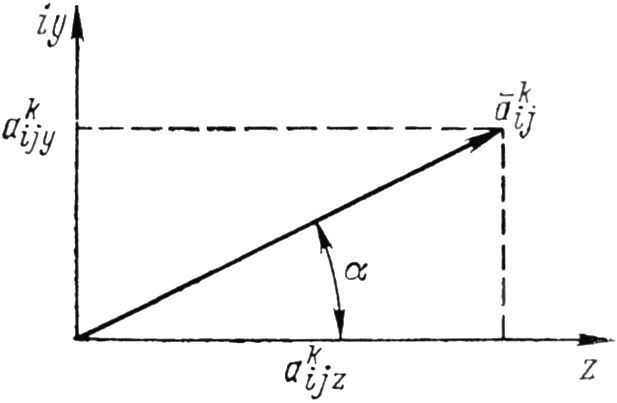
Рис. 15.27. Графическое построение к определению векторного коэффициента чувствительности.
В соответствии с рис. 15.27 имеем:
Тогда очевидно, что:
И выражение для функционала Uj принимает вид:
Теперь функционал Uj зависит уже от двух вещественных переменных Pjz и Pjy, вместо одной комплексной Рj.
Необходимое условие минимума функционала по переменной Pjz:
Отсюда получается вещественная часть оптимального корректирующего груза:
Необходимое условие минимума функционала по переменной Pjy:
Отсюда получается мнимая часть оптимального корректирующего груза:
Подставляя вещественное и мнимое значения корректирующего груза в формулу для Uj, получаем искомое минимальное значение функционала:
Указанные вычисления проводятся для всех:
Из этих вычисленных U(K)j min выбирается наименьшее — глобальный минимум K-то шага:
Из определения Uj следует, что:
Если характеризуемый величиной U(K)min уровень вибраций окажется неудовлетворительным, то, пользуясь вышеприведенной системой уравнений вычисления невязок, следует найти остаточные виброскорости и перейти к следующему K + 1-му шагу итерации, приняв в качестве начальных виброскоростей вычисленные на K-м шаге остаточные виброскорости.
Критерий удовлетворительности уровня вибрации выводится следующим образом. Полагаем, что точность измерения виброскоростей векторметрами оценивается 95%-ным доверительным интервалом. Тогда для ошибки ΔAi(0) измерения модуля начальной виброскорости A1 как известно, будем иметь:
Где σ — стандартное отклонение измерений модулей Ai(0) виброскоростей Āi(0).
Таким образом, приближенно имеем:
Для каждой итерации на основании полученных выше значений P(K)jz опт и P(K)jy опт после выбора оптимальной плоскости коррекции jопт вычисляются модуль оптимального корректирующего груза и фаза его радиус-вектора:
После подстановки значений:
В последние формулы имеем:
Приведенные соотношения являются расчетными формулами для всех K = 1, 2, …, S.
Уровень вибраций считается удовлетворительным, если выполняется соотношение:
Где:
— сумма квадратов начальных виброскоростей.
Продолжение расчета нецелесообразно, так как вероятность совпадения расчетных и измеренных остаточных виброскоростей, полученных при установке расчетной системы корректирующих масс, при дальнейших расчетах мала.
Если после K-й итерации уровень вибраций окажется неудовлетворительным, т. е. выполняется соотношение:
То прежде, чем переходить к K + 1-й итерации, следует проверить, имеется ли какой-нибудь существенный эффект от установки корректирующих грузов.
Критерием отсутствия существенного эффекта от установки корректирующих грузов является выполнение соотношения:
Если это соотношение выполняется, то расчет целесообразно прекратить. В противном случае следует перейти к K + 1-й итерации. Если хотя бы один из критериев прекращения итерационного процесса удовлетворяется, то в качестве окончательного минимального значения Umin функционала принимается полученное значение на последнем S-м шаге итерации.
Расчетно-теоретический анализ и опытные данные свидетельствуют о том, что относительное отклонение суммы квадратов виброскоростей малочувствительно к отклонению модуля корректирующего груза от оптимального значения (пологий экстремум). Например, уменьшение массы корректирующего груза на 45% приводит к увеличению суммы квадратов виброскоростей лишь на 20%.
Таким образом, при уменьшении масс корректирующих грузов, существенного ухудшения качества балансировки не происходит, а уменьшение их массы зачастую является целесообразным, так как ведет к улучшению динамических характеристик системы.
Рассмотренный итерационный метод расчета корректирующих грузов обладает следующими достоинствами:
1) он имеет высокую устойчивость решений и малое влияние погрешностей измерений, поскольку отсутствует прямое решение системы уравнений;
2) матрица коэффициентов чувствительности может иметь любое соотношение между количеством строк и столбцов; увеличение количества условий (количество строк), даже если они не являются независимыми, повышает качество и надежность процесса балансировки;
3) метод селективен к плоскостям коррекции: из любого количества плоскостей коррекции будут использованы только те, которые являются наиболее эффективными и обеспечивают требуемый конечный результат балансировки;
4) метод приводит к расчетным массам корректирующих грузов, как правило, значительно меньшим, чем при других методах расчета: исключается установка двух больших противофазных грузов в плоскостях, имеющих малоотличающиеся коэффициенты чувствительности.
Следует также отметить хорошее совпадение расчетных и действительных значений остаточных виброскоростей. Это является следствием как устойчивости метода, так и того, что погрешности в величине и угле установки грузов при малой их массе вносят значительно меньшие изменения остаточных вибраций.
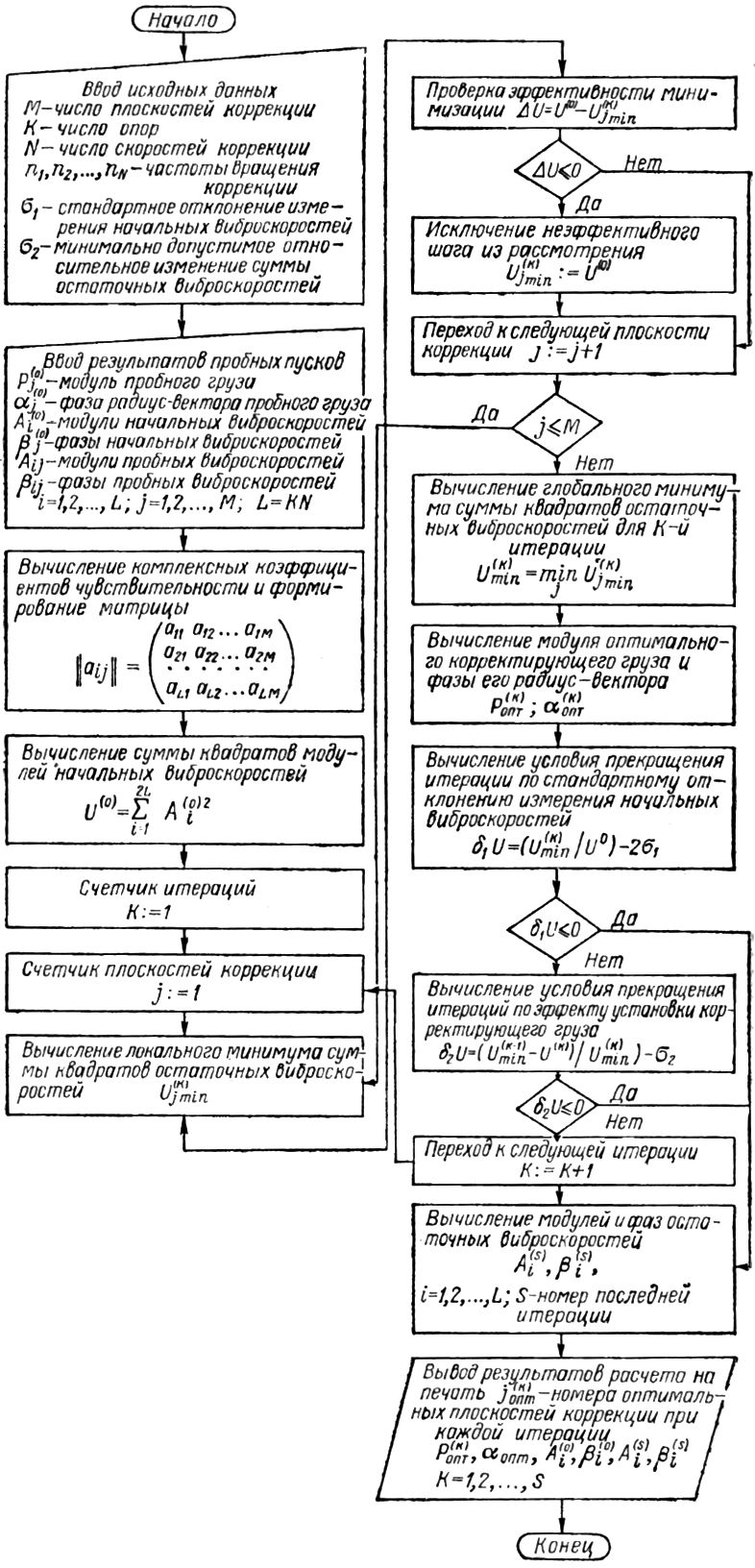
На рис. 15.28 приведена блок-схема алгоритма рассмотренного расчета корректирующих грузов.
Рис. 15.28. Блок-схема алгоритма расчета итерационным методом корректирующих грузов.
- Динамическая балансировка роторов паровых турбин: основные определения и используемое оборудование
- Динамическая балансировка роторов паровых турбин с расчетом коэффициентов чувствительности с оптимизацией по методу наименьших квадратов
- Пример расчета масс корректирующих грузов итерационным методом при динамической балансировке ротора низкого давления паровой турбины Т-100-130