Приведение статических моментов сопротивления к валу электродвигателя. Определение приведенного момента инерции электропривода.

Приведение статических моментов сопротивления к валу электродвигателя

Процесс приведения будем рассматривать на примере кинематической схемы механизма подъема крана.

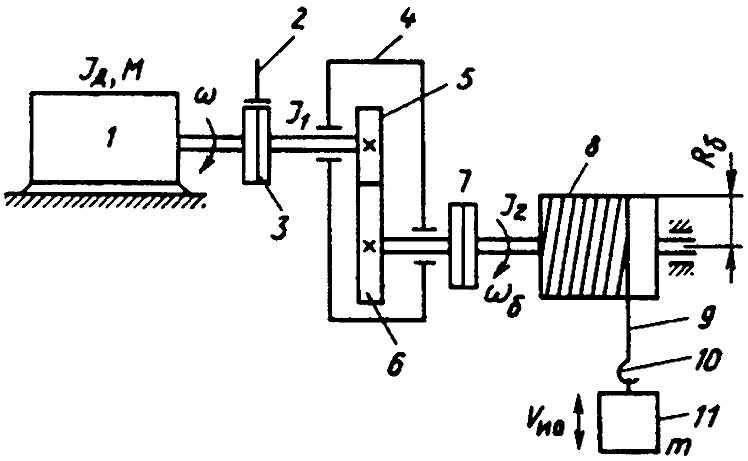
Кинематическая схема механизма подъема крана.

Для того чтобы перемещать груз с массой m со скоростью v_ио к нему должна быть приложена механическая мощность P_ио, равная произведению усилия, развиваемого при подъеме и скорости.

P_ио = F_ио·v_ио = m·g·v_ио

Во всех частях электропривода существуют потери, которые учитываются с помощью КПД. В нашей кинематической схеме суммарный КПД равен произведению КПД барабана на КПД редуктора.

η = η_б·η_р

В соответствии с законом сохранения энергии, необходимый момент, развиваемый двигателем должен обеспечивать необходимую мощность для перемещения груза.

M_с·ω = m·g·v_ио / η

Поделив обе части уравнения на ω, получим:

M_с = (mg / η)·(v_иоgρ / η)

M_с – момент сопротивления производственного механизма, приведен к валу двигателя от сил, совершающих поступательное движение.

v_ио/ω = ρ – радиус приведения.

Для того чтобы привести к валу двигателя моменты, действующие при вращательном движении рабочего органа, используем:

M_с·ω = M_ио·ω_б / η

M_с = M_ио·(ω_б / ω) / η

I = ω/ω_б – передаточное число.

M_с = M_ио / (η·i)

Чтобы привести к валу двигателя статические моменты, действующие в электродвигателе, не нужно знать тип передачи и количество ступеней передачи, а достаточно знать отношение скоростей на входе в привод и на его выходе – скорость вращения барабана.

Приведенный к валу двигателя статический момент исполнительного органа производственного механизма называется моментом сопротивления и обозначается M_с.

Определение приведенного момента инерции электропривода

В отличие от определения статического момента, для приведения динамического момента необходимо знать параметры механической передачи и тип передачи. Принцип приведения основан на том, что величина суммарного запаса кинетической энергии всех движущихся частей электропривода, приведенных к валу двигателя, остается неизменной.

J(ω²/2) = J_д(ω²/2) + J₅(ω²/2) + J₆(ω_б²/2) + J_б(ω_б²/2) + m(v²/2)

J(ω²/2) = (J_д + J₅)(ω²/2) + (J₆ + J_б)(ω_б²/2) + m(v²/2)

J_д + J₅ = J₁

J₆ + J_б = J₂

J₁ – момент инерции всех элементов привода, вращающихся со скоростью ω.
J₂ – момент инерции всех частей привода, совершающих вращательное движение со скоростью ω_б.

J(ω²/2) = J₁(ω²/2) + J₂(ω_б²/2) + m(v²/2)

J = J₁ + J₂(ω_б/ω)² + m(v/ω)²

J = J₁ + J₂/i² + mρ²

Для приведения суммарного момента инерции к валу двигателя нужно знать моменты инерции всех вращающихся элементов электрического привода и отношение скоростей между скоростью вращения двигателя и скоростью вращения элемента привода. Если они вращаются с разными скоростями, то момент инерции нужно разделить на передаточное число в квадрате, а момент инерции от массы всех частей электропривода, совершающих поступательное движение, для приведения умножить на квадрат радиуса приведения.