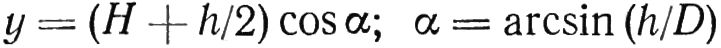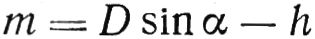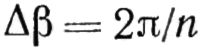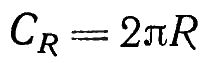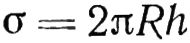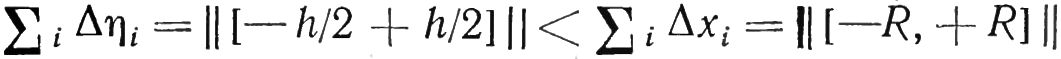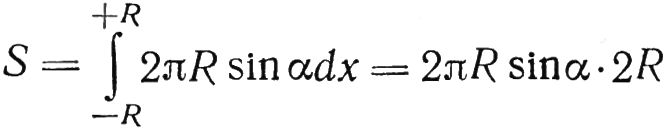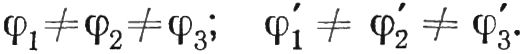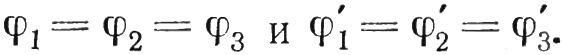Процесс механической обработки после заливки баббитом опорных вкладышей опорно-упорных подшипников паровых турбин значительно сложнее процесса обработки опорных вкладышей и в определенной своей части специфичен, на что и будет обращено внимание.
Процесс начинается с восстановления поверхности разъема путем фрезерования наплывов баббита с последующей припиловкой и пришабриванием. Восстанавливаются также совместной обработкой отверстия с точностью второго класса точности под болты и подгоняются пазы под соединения с подушками. После сборки на болтах в комплект нижняя и верхняя половины поступают на чистовую механическую обработку наружных поверхностей точением на токарно-лобовом или токарно-карусельном станках.
При установке выверкой достигают совмещения плоскости разъема с осью вращения шпинделя; с указанной осью совмещается и ось поверхности соединения основного материала вкладыша с баббитом. Только в этом случае у обработанного вкладыша слой баббита не будет иметь разной толщины.
Заданная овальность полости вкладышей достигается выполнением следующих приемов. После наружной чистовой механической обработки между стыковыми поверхностями разъема вкладышей устанавливаются мерные прокладки, толщина которых определена конструктором при проектировании подшипника паровой турбины. Таким образом, у собранного с прокладками вкладыша перед расточкой полости овальность перенесена на наружную поверхность.
При базировании на операции растачивания выверкой должно быть достигнуто параллельное расположение поверхностей разъема нижней и верхней половин вкладыша относительно оси вращения шпинделя станка. При этом ось шпинделя в вертикальном направлении должна находиться на одинаковых расстояниях от упомянутых поверхностей разъема, каждое из которых равно половине толщины прокладки. Так же должны быть равно удалены от оси шпинделя станка и диаметрально расположенные точки, находящиеся на наружной поверхности вкладыша непосредственно у разъема. Точность выверки должна находиться в пределах 0,03 мм.
Растачивание совмещено в одну операцию с точением торцовых поверхностей. Точность размеров взаимного расположения поверхностей и параметры шероховатости поверхностей должны находиться в пределах, установленных техническими требованиями.
После извлечения прокладок и повторной сборки со стыкованием по поверхности разъема наружные поверхности примут строго цилиндрическую форму, а овальность будет перенесена на полость.
Следующие операции — это растачивание только в верхней половине выемки, сверление отверстий со стороны торцовых поверхностей и со стороны разъема и нарезание в них резьб, фрезерование канавок и масляных карманов.
Наличие у опорных вкладышей и обойм опорно-упорных подшипников паровых турбин сферической поверхности делает необходимым включение в процесс специфических операций точения и шлифования по сфере.
Точение сферических поверхностей с небольшим припуском под шлифование выполнимо на токарных, токарно-лобовых или токарно-карусельных станках по следующим схемам. Обводом инструмента по контуру одновременно двумя подачами. При подаче, осуществляемой поворотом вокруг наклонной оси, пересекающейся в центре образуемой при механической обработке сферы с осью вращения шпинделя станка.
Существует несколько способов осуществления схем. Так как размеры детали подшипника паровой турбины со сферическими поверхностями имеют тенденцию к увеличению, то рассмотрение схем целесообразнее провести на примерах механической обработки на токарно-карусельных станках.
При механической обработке по первой схеме применены токарно-карусельные станки с устройствами механического, гидравлического и электрического копирования. Особенно целесообразно применение станков с контурным устройством ЧПУ. Размеры обрабатываемых деталей подшипников паровых турбин позволяют применять станки с диаметром планшайбы, не превышающим 1500 мм, т. е. модели 1516ФЗ, а также создаваемых на базе модели 1512. Обработка на станках с ЧПУ производится с высокой точностью, достигающей 0,06 мм. Это позволяет назначать минимальный припуск на последующее шлифование, равный 0,1 мм на сторону.
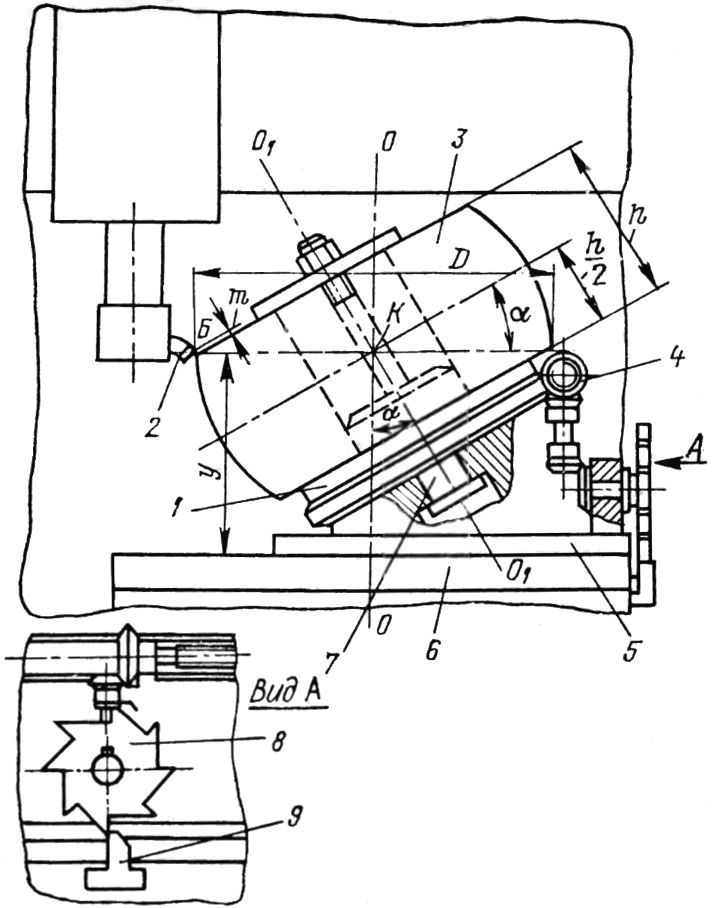
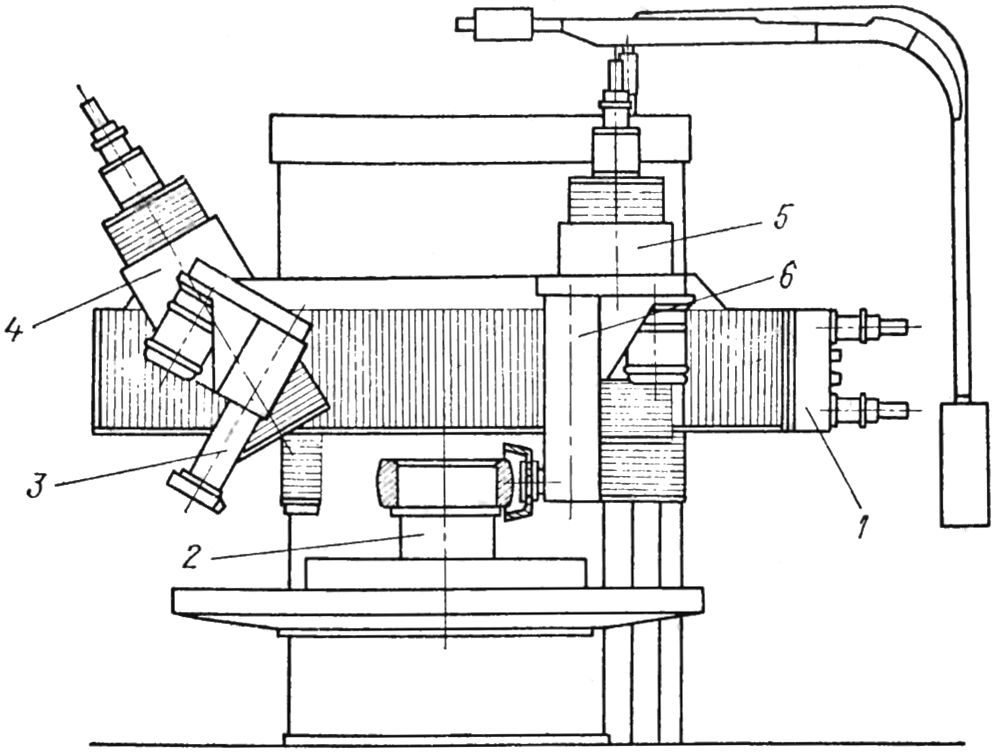
Разновидностью рассматриваемой схемы механической обработки сферической поверхности обводом инструмента по контуру одновременно двумя подачами является процесс точения на модернизированном токарно-карусельном станке, изображенном на рис. 5.5.
Рис. 5.5. Модернизированный токарно-карусельный станок для механической обработки сферических поверхностей вкладышей подшипников паровых турбин и обойм вкладышей.
На неподвижной стержневидной формы стойке 1, тело которой пропущено сквозь полость шпинделя, шарнирно закреплен рычаг 4 с суппортом 5, несущим резец. На рисунке станок показан настроенным на обработку наружной сферы детали паровой турбины. Поэтому направленный к обрабатываемой поверхности резец обращен в сторону оси вращения шпинделя станка. При механической обработке внутренней сферической поверхности перемещающаяся часть суппорта повернута на 180°. Базой являются торец и полость, которыми вкладыш устанавливается на сменную подставку — приспособление 2. Следует отметить, что опорная поверхность приспособления должна находиться на строго определенном расстоянии от оси поворота рычага, равного расстоянию от торца вкладыша до оси сферы. При соблюдении этого правила центр полученной обточкой сферической поверхности будет находиться на заданном чертежом расстоянии от торцовой поверхности детали, выбранной за базу. Движение подачи инструменту сообщается от коробки подач станка при вертикальном перемещении ползуна, шарнирно связанного с рычагом устройства. Способ менее точен и обеспечивает обработку с допуском 0,1—0,12 мм. На этом же станке осуществляется и шлифование сферической поверхности шлифовальной бабкой 3.
Обработка по второй схеме осуществляется на модернизированном токарно-карусельном станке. На нем возможна механическая обработка наружной и внутренней сферических поверхностей турбинных подшипников как в режиме дискретной, так и в режиме непрерывной подачи. Рассмотрим более простой случай обработки с дискретной подачей наружной сферической поверхности, поясненный схемой наладки модернизированного станка (рис. 5.6).
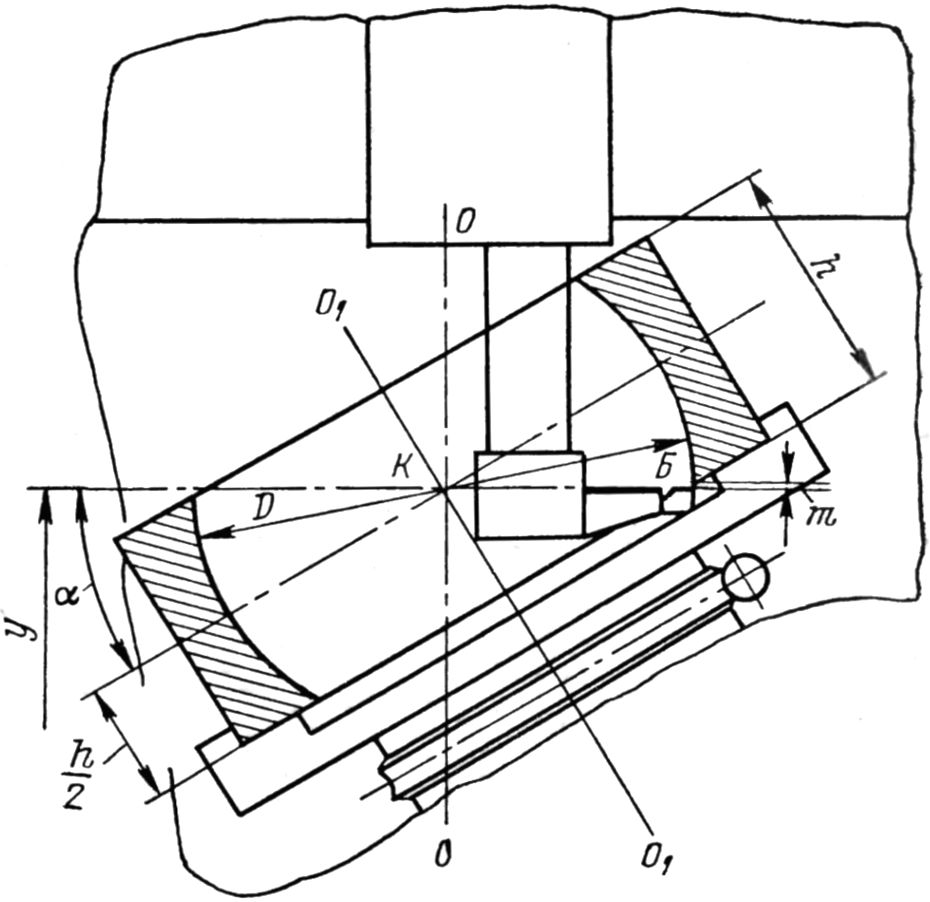
Рис. 5.6. Схема наладки модернизированного токарно-карусельного станка для механической обработки сферической поверхности обойм вкладышей и вкладышей подшипников паровых турбин при круговой подаче вокруг наклонной оси.
На планшайбе 6 станка установлена платформа 1, ее поверхность к поверхности планшайбы наклонена так, что ось O—O вращения планшайбы и ось O1—O1 поворота платформы в точке К пересекаются.
Платформа установлена на основании 5 и снабжена осью 7. Ободу платформы приданы элементы червячного колеса, зубцы которого сцеплены с червяком, являющимся звеном передачи 4. Движение на червяк передаетcя вращающимся совместно с планшайбой станка упором 9 на звездочку 8 и далее от периодически поворачивающейся на шаг зуба звездочки двумя парами конических шестерен на вал червяка. В приспособлении, размещенном на платформе, устанавливается обрабатываемая деталь 3.
В исходном положении платформа наклонена на угол α таким образом, чтобы точка К была удалена от поверхности планшайбы станка на величину y, которая, как и угол α, определяется из условий:
Где H — расстояние до плоскости основания от поверхности платформы, измеренное по оси O1—O1; h — высота сферического пояса; D — диаметр сферы.
Для упрощения принято, что сферический пояс симметричен относительно диаметрального сечения.
Резец 2 установлен таким образом, что точка Б его вершины совмещена с линией, проходящей параллельно плоскости планшайбы через точку К на расстоянии D/2 от оси O—O. Так как рассматривается случай дискретного изменения подачи, то необходимо приращение подачи осуществлять в то время, когда не происходит процесс резания. Поэтому точка Б — вершина резца — размещена на расстоянии m от верхнего торца детали, при этом его значение строго определенно и рассчитано по формуле:
Для механической обработки детали паровой турбины сообщается главное движение — вращение планшайбы станка вокруг оси O—O. Резец пройдет расстояние m без снятия стружки, а затем врежется в заготовку и оставит на ней строчку, диаметр впадины которой будет равен диаметру D сферы. Когда же резец вновь будет находиться в пределах зазора, один из зубцов звездочки войдет в контакт с упором, вследствие чего в процессе продолжающегося вращения планшайбы звездочка повернется на часть оборота и через механизм переместит платформу с деталью на заданную угловую подачу. За второй оборот планшайбы станка деталь будет обработана по второй строчке до диаметра D сферы. Аналогичным образом за один оборот платформы деталь будет обработана по всей сферической поверхности.
Рис. 5.7. Схема наладки модернизированного токарно-карусельного станка на обработку внутренней сферической поверхности вкладышей подшипников и обойм вкладышей паровых турбин при круговой подаче вокруг наклонной оси.
Схема наладки модернизированного токарно-карусельного станка на механической обработку внутренней сферической поверхности изображена на рис. 5.7. На этой схеме приняты те же обозначения, что и на схеме рис. 5.6. Все сказанное для случая обработки наружной сферической поверхности справедливо и для обработки внутренней сферы. Этот способ гарантирует высокую точность, зависящую в основном от точности станка. Достижима обработка сферы с соблюдением допуска 0,06 мм. Рис. 5.8 и расчеты к нему доказывают, что образованная вышеописанным способом поверхность представляет собой сферический пояс как при дискретной, так и при непрерывной подачах.
Рис. 5.8. Графические построения к доказательству образования сферической поверхности при точении с угловой подачей вокруг наклонной оси.
На основной левой части рисунка представлено, в соответствии со схемой механической обработки, положение детали подшипника турбины. Для упрощения высота шарового пояса принята симметрично распределенной относительно плоскости большого круга, проходящей через центр сферы O перпендикулярно к оси вращения Oη в процессе круговой подачи в направлении β.
При точении очередной канавки в режиме дискретной подачи, т. е. когда поворот детали на угол подачи:
Вокруг оси Oη происходит вне процесса резания, подача равна нулю. За один оборот детали вокруг оси OY резец образует на ее поверхности канавку длиной, равной длине окружности большого круга.
Затем так же вне процесса резания производится очередной шаг подачи. Далее цикл повторяется необходимое число раз до полной механической обработки всего шарового пояса.
При непрерывной подаче за один оборот детали вокруг оси OY резец точит на ее поверхности канавку, ось которой представляет собой один виток спирали с шагом, определяемым угловой подачей, равной β [рад·об-1]. Далее цикл повторяется столько раз, сколько необходимо для механической обработки всего шарового пояса.
Необходимо доказать, что в первом приближении площадь шарового пояса в пределе может быть полностью покрыта совокупностью канавок, протачиваемых резцом, если считать, что ширина канавки сколь угодно мала, а их число сколь угодно велико.
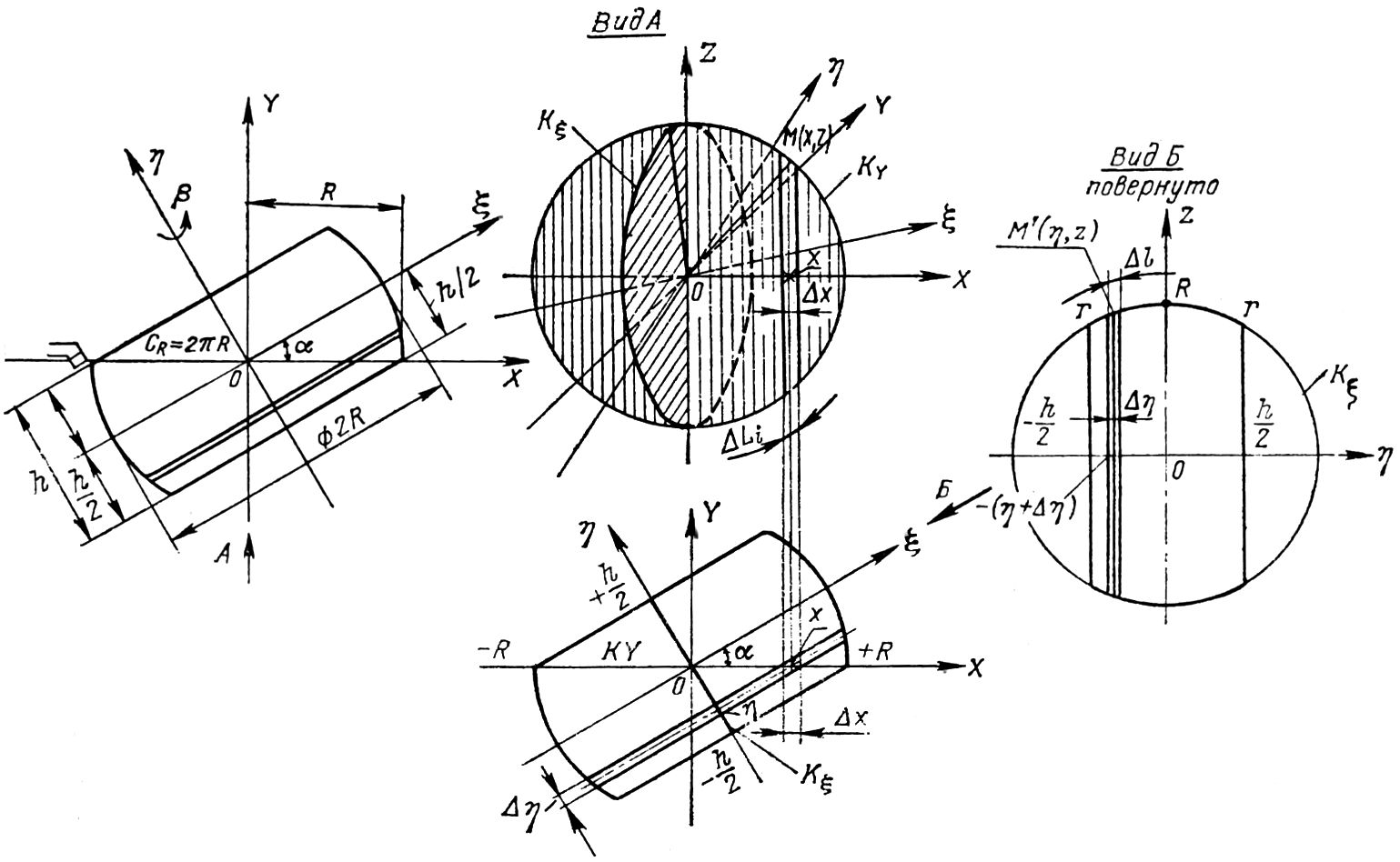
Обратимся к виду А на рис. 5.8. На нем KY — это окружность большого круга основной сферы радиуса R. Из рисунка видно также, что ось Oη не лежит в плоскости круга KY, не перпендикулярна к ней, а занимает некоторое промежуточное положение.
Пусть круг KY вращается вокруг оси Oη с некоторой угловой скоростью β. При этом окружность KY описывает некоторую поверхность S. Вычислим площадь полученной таким образом поверхности S.
Проведенное исследование показывает, что S = σ;
Где σ — площадь поверхности шарового пояса; h — высота поверхности шарового пояса.
Идея доказательства заключается в сведении исходной задачи к эквивалентной ей, но более наглядной и состоит в следующем. Представим, что круг KY разделен хордами параллельно оси OZ на некоторое число полос. Возьмем какую-нибудь полосу и спроектируем ее на плоскость ηOZ. На рисунке этот процесс упрощен и сводится к представлению в плане спроектированного отрезка ΔX — следа нашей полосы — с оси OX на ось Oη — отрезка Δη. Дальнейший ход рассуждений будет увязан с видом по стрелке Б в плоскости ηOZ. Вращая полосу шириной Δη вокруг оси Oη, получим элементарное тело вращения, поверхность которого образуется дугой Δli.
Проектируя точно так же все остальные полосы на плоскость ηOZ, убедимся, что проекция отрезка [-R, +R] оси OX на ось Oη будет отрезком [-h/2, +h/2].
Теперь уже очевидно, что при своем вращении вокруг оси дуга rr = ΣiΔli опишет рассматриваемый шаровой пояс.
Остается доказать, что полученная задача эквивалентна исходной. Из рис. 5.8 (вид А) ясно, что при любых π/2 > α > 0 имеем:
Откуда:
И соответственно площадь криволинейного четырехугольника (вид Б) меньше площади круга KY (вид А).
Процесс вращения криволинейного четырехугольника вокруг оси Oη (вид Б) можно мысленно раздробить на совокупность независимых вращений каждой полосы и рассматривать полученную поверхность вращения как совокупность элементарных поверхностей вращения, полученных от отдельных полос. Такое же мысленное дробление проведем и для круга KY (вид А).
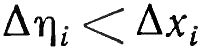
Очевидно, что каждая полоса круга шире соответствующей полосы четырехугольника (вид Б). Так как все дуги на обоих рисунках имеют один и тот же радиус R, то каждая дуга ΔLi (вид А), ограничивающая полосу круга, длиннее соответствующей дуги Δli (вид Б) четырехугольника. Но тогда неясно, будут ли равны между собой площади боковых поверхностей, образуемых обеими фигурами. Для выяснения этого используем следующий прием. Будем неограниченно уменьшать ширину Δx (вид А) каждой полосы. При этом соответственно будет уменьшаться ширина каждой из полос Δη. В пределе при Δx → 0 каждая полоса шириной Δx превратится в линию, след которой станет точкой x на оси OX.
Так как Δη < Δx, то при Δx → 0 подавно будет Δη → 0, и каждая полоса шириной Δη постепенно также перейдет в линию, след которой станет точкой η на оси Oη. При этом очевидно, что между точками отрезков [-R, +R] и [-h/2, +h/2] устанавливается взаимно однозначное соответствие. В теории множеств доказывается, что тогда оба множества точек равномощны (как бы равночисленны). Следовательно, в пределе сведение одной задачи к другой правомерно, и вычисление площади искомой поверхности сводится к интегрированию.
Уравнение окружности KY в системе XOZ будет: х2 + z2 = R2. Отсюда ордината z произвольной точки M окружности KY получается в виде z = √(R2 — x2). Соответствующая точке M точка окружности k имеет ординату в системе ηOZ z = √(R2 — η2).
Опуская промежуточные выкладки, получаем, что площадь AS элементарной боковой поверхности, образованной вращанием элементарной дуги Δl (вид Б) будет ΔS = 2πR sin α Δx.
Переходя в обеих частях этой формулы к пределу Δx → 0 и интегрируя по x от -R до +R, находим:
Здесь 2R sin α = h.
Таким образом, S = 2πRh и доказано, что S = σ.
Следовательно, окружность KY (вид А) при своем вращении вокруг оси Oη действительно описывает боковую поверхность шарового пояска. Значит, шаровой пояс полностью покрывается бесконечным множеством окружностей больших кругов KY, плоскости которых расположены под углом α ≠ 0 к экваториальной плоскости исходного шара при непрерывной подаче. Этот же результат получается как предел при дискретной подаче, при неограниченном уменьшении ее шага, так как в пределе при Δβ → 0 различие между непрерывной и дискретной подачами исчезает.
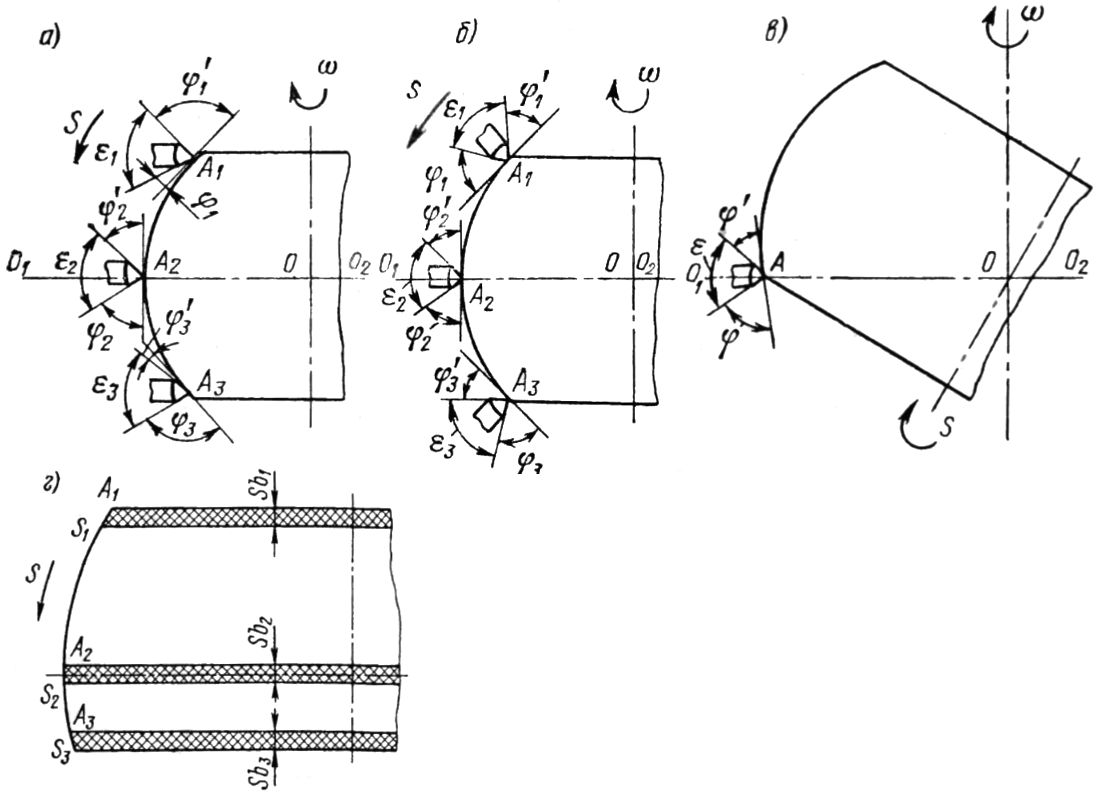
Процесс резания при обработке сферических поверхностей вкладышей подшипников у паровых турбин по рассмотренным схемам протекает в разных условиях. Для пояснения этих условий на рис. 5.9 представлена серия построений. На них показана обработка наружных сферических поверхностей. Но все это справедливо и для процесса механической обработки внутренних поверхностей.
Рис. 5.9. Графические построения к технологическим схемам обработки сферических поверхностей вкладышей подшипников и обойм паровых турбин.
На всех графических построениях одинаково обозначены: O1—O2 — след плоскости, пересекающий сферу через центр O, т. е. совмещенной с плоскостью сечения по большому кругу; ε — угол резца при вершине; φ — главный угол в плане; φ’ — вспомогательный угол в плане; ω← — направление главного движения; s← — направление движения подачи.
На рис. 5.9, а изображено положение инструмента при обводе по поверхности сферы двумя подачами по копиру или при механической обработке на станке с ЧПУ. Рис. 5.9, б показывает положение инструмента при обработке с перемещением резца по окружности, центр которой совмещен с центром O сферы.
Нетрудно заметить, что резание по схемам рис. 5.9, а, б при условии сохранения постоянства частоты вращения планшайбы токарно-карусельного станка будет проходить с переменной скоростью по мере продвижения резца от точки А1 через А2 к А3. Она будет изменяться пропорционально изменению радиуса окружности, образованной в местах пересечений сферической поверхности с плоскостями сечений, перпендикулярных к оси вращения шпинделя. Наибольшего значения скорость резания достигнет при механической обработке поверхности в непосредственной близости от сечения по большому кругу, т. е. от точки А2. (Для конкретных размеров вкладышей опорно-упорных подшипников паровых и газовых турбин скорость резания изменяется в пределах до 15%.)
По этому же закону и в тех же пределах изменяется скорость резания при механической обработке с поворотом резца вокруг точки O — центра сферической поверхности, т. е. при перемещении резца, как это показано на рис. 5.9, б.
Скорость резания при обработке по схеме, изображенной на рис. 5.9, в, остается неизменной в течение всего процесса.
Следовательно, если при механической обработке по первым двумя схемам не может быть сохранена (без применения устройств бесступенчатого изменения скорости главного движения) оптимальная постоянная скорость резания в течение всего процесса, то при обработке по третьей схеме это условие может быть выполнено.
Направление подачи при перемещении инструмента в соответствии со схемами на рис. 5.9, а, б — это движение по окружности с центром в точке О.
При механической обработке на станке с копирным устройством (вариант схемы рис. 5.9, а) перемещение инструмента достигается сложением скоростей двух движений: вертикального с постоянной скоростью подачи, сообщаемого от коробки подач ползуну суппорта, и горизонтального — вдоль траверсы станка, повторяющего движения в горизонтальном направлении ощупывающего элемента копирного устройства. Так как вторая составляющая переменная, то и слагаемая скорость обвода инструментом обрабатываемой поверхности будет переменной.
Характер изменения скорости подачи для рассматриваемого случая пояснена на рис. 5.9, г. Высота заштрихованных шаровых поясов у точек А1—А3 имеет одно и то же значение, равное осевой вертикальной составляющей подачи: sb1 = sb2 = sb3.
Однако при движении по копиру резец на равных отрезках вертикальных перемещений будет проходить различные дуги, а, следовательно, равные отрезкам дуг круговые подачи также различны. При этом всегда будут сохраняться зависимости s2 < s1; s2 < s3.
Рассчитанное для конкретных размеров сфер и высот сферических поясов вкладышей опорно-упорных подшипников паровых турбин отклонение величин подач от оптимального значения находится в пределах до 15%. Переменна и изменяется в тех же пределах подача и при механической обработке по схеме, изображенной на рис. 5.9, б.
Как уже было отмечено, схема рис. 5.9, а отражает процесс обработки сферических поверхностей вкладышей турбинных подшипников на токарно-карусельных станках с ЧПУ. Но изменением сообщаемых рабочим органам станка с ЧПУ взаимоувязанных скоростей перемещений в горизонтальном и вертикальном направлениях можно достичь постоянства оптимального значения скорости обвода — подачи — по контуру от точки А1 через А2 к точке А3.
Движение подачи при механической обработке по схеме (рис. 5.9, в) осуществляется с постоянной угловой скоростью. В течение одного оборота детали вокруг оси главного движения ширина срезаемого слоя металла дважды изменяется от своего наибольшего значения до нуля.
По рис. 5.9 можно проследить и за изменением влияющих на процесс резания углов в плане: главный угол φ, вспомогательный угол φ’ и угол ε при вершине. Обозначение точек сохранено и в приложении к рассматриваемым углам.
Углы φ и φ’ определяются положением инструмента и положением касательной к окружности, образованной секущей вертикальной плоскостью, проходящей через центр О сферы и вершину резца.
Примем положение инструмента в точке А2 (рис. 5.9, а) и соответствующие этому положению углы φ2 и φ2‘ за исходные номинальные. Тогда в точках А1 и А2 названные углы получат обозначения соответственно φ1 и φ1‘ φ3 и φ3‘.
При точении по копиру и по программе на станке с ЧПУ механическая обработка производится без поворота вершины резца относительно точки O сферы. Положение касательной к окружности, образованной секущей плоскостью, проходящей через точку O сферы и вершину резца изменяется, а, следовательно, изменяется и значение углов:
Если резцы заточить с образованием рекомендуемых оптимальных для резания значений главного φ, вспомогательного φ’ углов в плане и угла ε при вершине, то указанные значения углов φ и φ’ при обработке сферы по рассматриваемым схемам сохранятся только при положении резца в точке А2. В точке А1 значение угла φ будет минимальным, а угла φ’ максимальным. В точке А2, наоборот, угол φ примет наибольшее, а угол φ’ наименьшее значения. Углы φ и φ’ при этом будут иметь такие значения, что процесс резания становится неэффективным. Для частичной оптимизации процесса резания на участках, близких к точкам А1 и А3, приходится заведомо ухудшать геометрические параметры резца за счет увеличения против рекомендуемых значений углов φ и φ’в плане, а следовательно, и уменьшения против нормы угла ε при вершине. А это приводит к снижению стойкости инструмента и к понижению достигнутого параметра шероховатости.
Иная картина при механической обработке сферической поверхности деталей вкладышей паровых турбин на модернизированном токарно-карусельном станке с поворотом вершины резца вокруг точки O сферы (рис. 5.9, б). В процессе обвода:
Рассматриваемая схема не накладывает ограничений на выбор геометрии в плане режущей части инструмента. Схема рис. 5.9, в также не накладывает ограничений на выбор геометрии в плане режущей части резца и обеспечивает сохранность углов в плане в течение всего процесса.
Шлифование сферических поверхностей осуществляется на модернизированных токарных, токарно-карусельных либо на специализированных карусельно-шлифовальных станках. Во всех случаях этот процесс основан на принципе образования окружности при сечении шара плоскостью.
Если к вращающейся со скоростью подачи вокруг оси полости вкладыша турбинного подшипника с предварительно образованной точением сферической поверхностью подвести вращающийся со скоростью главного движения чашечной формы шлифовальный круг, то образованная в процессе этих двух движений поверхность будет иметь форму шарового пояса. При этом должны соблюдаться и дополнительные условия. Центр образованной шлифованием сферы, относительно взятой за базу торцовой поверхности вкладыша, будет находиться на заданном расстоянии только в том случае, если ось вращения шлифовального круга пересечется с осью вращения шпинделя станка на том же расстоянии от принятой за базу поверхности. У шлифовального круга диаметр шлифующей кромки должен быть не меньше двойной высоты наибольшей от оси сферы части шарового пояса.
На модернизированном токарно-карусельном станке (рис. 5.5) в одной многоцелевой операции возможны точение и шлифование шаровых поверхностей. Для этого во второй суппорт станка помещена шлифовальная головка 3, состоящая из электродвигателя, на валу которого установлен собранный из сегментов шлифовальный круг. Из зоны резания абразивная пыль и стружка удаляются через шланг помещенной у станка установкой для отсоса.
На рис. 5.10 изображена одна из моделей универсального карусельно-шлифовального станка, на котором возможно и шлифование сферических поверхностей деталей паровых турбин. На траверсе 1 станка помещены бабки 4 и 5 со шпиндельными головками 3 и 6. Деталь установлена на приспособлении 2. В приспособлении шлифуемая деталь базируется на торцовую поверхность. Выверка положения детали турбины осуществляется ее перемещением по плоской поверхности приспособления до совмещения оси полости с осью шпинделя планшайбы станка и контролируется индикатором, закрепленным на шпиндельной головке. Допустимое несовмещение оси шпинделя планшайбы и детали 0,01 мм.
Рис. 5.10. Карусельно-шлифовальный станок для обработки сферических поверхностей вкладышей подшипников и обойм подшипников паровых турбин.
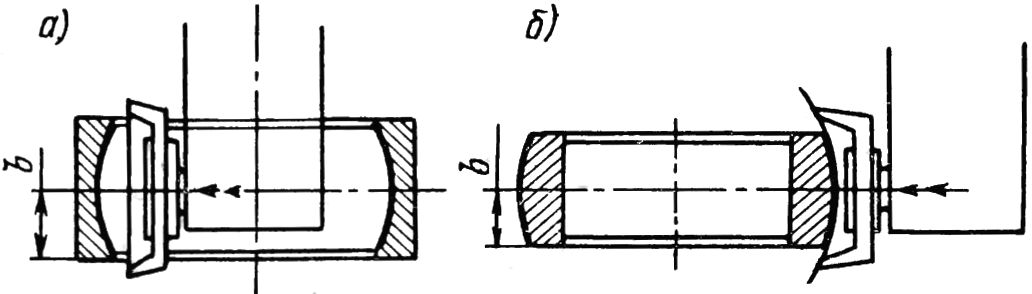
На рис. 5.11, а показана схема наладки на шлифование внутренних сферических поверхностей, а на рис. 5.11, б — наружных. Направление перемещения кругов при настройке и при врезании в процессе резания вдоль оси шпинделя шпиндельной головки указано стрелками.
Рис. 5.11. Схема наладки карусельно-шлифовального станка для обработки сферических поверхностей вкладышей подшипников и обойм паровых турбин.
Ось вращения шпинделя шпиндельной головки в процессе шлифования всегда находится в площади большого круга образуемой сферической поверхности. Поэтому правильное заданное чертежом положение центра обработанной сферы может быть достигнуто размещением при настройке оси шпинделя шпиндельной головки на расстоянии от приспособления, равном размеру b положения центра сферической поверхности детали относительно ее торца, принятого за базу.
Процесс окончательного шлифования крупных, вкладышей подшипников у паровых турбин выполняется при следующих режимах: скорость резания, определяемая частотой вращения шлифовального круга, 35—40 м/с; поперечная подача 0,005—0,009 мм/об; подача, определяемая частотой вращения детали, 60—70 м/мин. Достижимая точность шлифования 0,01 мм, достижимый параметр шероховатости Ra = 1,25 мкм.